The Implementation of Generative Pre-trained Transformers (GPT)#
Dependencies#
Show code cell content
from __future__ import annotations
import os
import random
import time
import warnings
from pathlib import Path
from typing import Any, Dict, List, Literal, Optional, Tuple, Union
import matplotlib.pyplot as plt
import numpy as np
import requests
import seaborn as sns
import tiktoken
import torch
import torch.backends.cudnn
import torch.nn.functional as F
from numpy.typing import ArrayLike, NDArray
from pydantic import BaseModel, Field, computed_field, model_validator
from rich.pretty import pprint
from torch import nn
from torch.utils.data import DataLoader, Dataset
Composing the Configurations#
class Composer(BaseModel):
seed: int = 2024
debug: bool = False
url: str = "https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt"
dataset_name: str = "tinyshakespeare"
data_folder: str = Field(default="./data/tinyshakespeare", description="Path to the data folder")
train_path: Path = Field(None, description="Path to the train file")
valid_path: Path = Field(None, description="Path to the valid file")
encoding_name: Literal['gpt2', 'r50k_base', 'p50k_base', 'p50k_edit', 'cl100k_base'] = "gpt2"
batch_size: int = Field(default=64, description="Batch size")
block_size: int = Field(default=128, description="Block size, an alias for max length/context window size.", alias="context_length")
device_type: Literal["cpu", "cuda"] = "cpu"
device: torch.device = Field(None, description="Device to use")
# model parameters
d_model: int = Field(default=512, description="Dimension of the model")
d_ff: int = Field(default=512, description="Dimension of the feed forward layer")
H: int = Field(default=8, description="Number of heads", alias="num_heads")
vocab_size: int = Field(default=50257, description="Vocabulary size")
num_decoder_blocks: int = Field(default=6, description="Number of decoder blocks")
@model_validator(mode="after")
def set_train_valid_paths(self) -> Composer:
self.train_path = Path(self.data_folder) / "train.bin"
self.valid_path = Path(self.data_folder) / "valid.bin"
return self
@model_validator(mode="after")
def set_device(self) -> Composer:
self.device = torch.device(self.device_type)
return self
@model_validator(mode="after")
def set_debug_fields(self) -> Composer:
if self.debug:
self.batch_size = 2
self.block_size = 8
self.d_model = 4
self.H = 2
self.d_ff = 4
return self
class Config:
extra = "allow"
arbitrary_types_allowed = True
composer = Composer(debug=True)
pprint(composer)
Composer( │ seed=2024, │ debug=True, │ url='https://raw.githubusercontent.com/karpathy/char-rnn/master/data/tinyshakespeare/input.txt', │ dataset_name='tinyshakespeare', │ data_folder='./data/tinyshakespeare', │ train_path=PosixPath('data/tinyshakespeare/train.bin'), │ valid_path=PosixPath('data/tinyshakespeare/valid.bin'), │ encoding_name='gpt2', │ batch_size=2, │ block_size=8, │ device_type='cpu', │ device=device(type='cpu'), │ d_model=4, │ d_ff=4, │ H=2, │ vocab_size=50257, │ num_decoder_blocks=6 )
Reproducibility#
def configure_deterministic_mode() -> None:
# fmt: off
torch.use_deterministic_algorithms(True, warn_only=True)
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.enabled = False
os.environ['CUBLAS_WORKSPACE_CONFIG'] = ':4096:8'
# fmt: on
warnings.warn(
"Deterministic mode is activated. This will negatively impact performance and may cause increase in CUDA memory footprint.",
category=UserWarning,
stacklevel=2,
)
def seed_all(
seed: int = 1992,
seed_torch: bool = True,
set_torch_deterministic: bool = True,
) -> int:
# fmt: off
os.environ["PYTHONHASHSEED"] = str(seed) # set PYTHONHASHSEED env var at fixed value
np.random.default_rng(seed) # numpy pseudo-random generator
random.seed(seed) # python's built-in pseudo-random generator
if seed_torch:
torch.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # pytorch (both CPU and CUDA)
torch.backends.cudnn.deterministic = True
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.enabled = False
if set_torch_deterministic:
configure_deterministic_mode()
# fmt: on
return seed
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
2024
Utilities#
def am_i_in_jupyter() -> bool:
try:
from IPython import get_ipython
if "IPKernelApp" not in get_ipython().config:
return False
except ImportError:
return False
return True
IN_JUPYTER = am_i_in_jupyter()
Tokenization and Vocabulary#
Traditional tokenization methods often involve steps such as lower-casing, punctuation stripping, and splitting on whitespace. Additionally, these methods might encode out-of-vocabulary words using a special token to enable the model to handle unseen words during evaluation or testing phases. For instance, language models (LMs) may struggle with interpreting emojis due to such constraints.
These conventional approaches can inadvertently restrict the natural language input space \(\mathcal{X}\), consequently limiting the model space \(\mathcal{H}\). This limitation stems from the fact that the scope of \(\mathcal{H}\) is inherently dependent on the comprehensiveness of \(\mathcal{X}\) as we can see \(\mathcal{H} = \mathcal{H}(\mathcal{X} ; \boldsymbol{\Theta})\), which means that the model space \(\mathcal{H}\) is a function of the input space \(\mathcal{X}\) and the parameter space \(\boldsymbol{\Theta}\).
To resolve this, the idea of byte-level encoding can be used - since you theoretically can encode any character in the world in UTF-8 encoding.
However, the limitation is current byte-level language models tend to perform poorly on word level tasks.
The authors then introduced the BPE algorithm (is “byte-level” because it operates on UTF-8 encoded strings) where they striked a balance between character-level and word-level tokenization.
So in summary, BPE is the tokenizer used to encode the input text into a sequence of tokens - which form the input representation to the model.
Byte pair encoding (BPE) is a way of converting text into tokens and is used as the tokenizer in the training of GPT-2. It has a couple desirable properties[1]:
It’s reversible and lossless, so you can convert tokens back into the original text
It works on arbitrary text, even text that is not in the tokeniser’s training data
It compresses the text: the token sequence is shorter than the bytes corresponding to the original text. On average, in practice, each token corresponds to about 4 bytes.
It attempts to let the model see common subwords. For instance, “ing” is a common subword in English, so BPE encodings will often split “encoding” into tokens like “encod” and “ing” (instead of e.g. “enc” and “oding”). Because the model will then see the “ing” token again and again in different contexts, it helps models generalise and better understand grammar.
We first download the dataset from the Karpathy’s repo.
def download(url: str, dataset_name: str, dest_folder: Path | str) -> Tuple[Path, str]:
dest_folder_path = Path(dest_folder)
dest_folder_path.mkdir(parents=True, exist_ok=True)
filepath = dest_folder_path / f"{dataset_name}.txt"
response = requests.get(url, stream=True, timeout=30)
corpus = response.text
response.raise_for_status()
with open(filepath, "wb") as f:
for chunk in response.iter_content(chunk_size=8192):
f.write(chunk)
return filepath, corpus
filepath, corpus = download(composer.url, composer.dataset_name, composer.data_folder)
pprint(filepath)
PosixPath('data/tinyshakespeare/tinyshakespeare.txt')
We print the first \(100\) characters from the corpus below.
print(corpus[:100])
First Citizen:
Before we proceed any further, hear me speak.
All:
Speak, speak.
First Citizen:
You
We print out all Tiktoken encodings, and note to ourself that we will be using
gpt2 - in which the vocabulary size \(\lvert \mathcal{V} \rvert = 50257\).
print(f"All TikToken encodings: {tiktoken.list_encoding_names()}")
# encode with tiktoken gpt2 bpe
tokenizer = tiktoken.get_encoding(composer.encoding_name)
print(f"Vocabulary size: {tokenizer.n_vocab}")
All TikToken encodings: ['gpt2', 'r50k_base', 'p50k_base', 'p50k_edit', 'cl100k_base']
Vocabulary size: 50257
We then slice the corpus into train-valid subsets with a ratio of
\(9:1\).
N = len(corpus)
train_data = corpus[: int(N * 0.9)]
valid_data = corpus[int(N * 0.9) :]
We then encode train_data and valid_data using the tokenizer.
train_ids = tokenizer.encode_ordinary(train_data)
valid_ids = tokenizer.encode_ordinary(valid_data)
print(f"train has {len(train_ids):,} tokens")
print(f"val has {len(valid_ids):,} tokens")
train has 301,966 tokens
val has 36,059 tokens
print(tokenizer.decode(train_ids[:2]))
print("-" * 80)
print(tokenizer.decode(train_ids[:100]))
First Citizen
--------------------------------------------------------------------------------
First Citizen:
Before we proceed any further, hear me speak.
All:
Speak, speak.
First Citizen:
You are all resolved rather to die than to famish?
All:
Resolved. resolved.
First Citizen:
First, you know Caius Marcius is chief enemy to the people.
All:
We know't, we know't.
First Citizen:
Let us kill him, and we
Lastly, we save the tokenized corpus into .bin file for later usage.
# export to bin files
train_ids = np.array(train_ids, dtype=np.uint16)
valid_ids = np.array(valid_ids, dtype=np.uint16)
train_ids.tofile(composer.train_path)
valid_ids.tofile(composer.valid_path)
# train.bin has 301,966 tokens
# val.bin has 36,059 tokens
Dataset and Dataloading (Poor Man’s Dataloader)#
To batch the corpus into mini-batch of \(\mathcal{B}\) for training using PyTorch
framework, we would need to create an efficient way of loading. The easy way out
is of course to use PyTorch’s Dataset class and work from there, but to keep
this post similar to what Karpathy used, we would try to understand how he
approached it.
As Karpathy puts it, he implemented a poor man’s
dataloader.
We will start by dissecting the code and understanding how it works and finally,
show that everything can be done with PyTorch’s Dataset and Dataloader.
Memory Mapping#
Firstly, Karpathy uses numpy’s
memory mapping
(numpy.memmap) to load the data. Memory mapping is used to create a
memory-mapped array from a binary file. This involves mapping the contents of a
file directly into the virtual memory space of the calling process. This allows
applications to access the file data as if it were loaded in memory, using
pointer operations or array indexing, without the need for explicit read or
write operations.
This essentially means that you can access small segments of a large file without having to load the entire file into memory. The concept draws similarities to the use of generators in Python, where you can iterate over a large dataset without having to load the entire dataset into memory.
train_data = np.memmap(composer.train_path, dtype=np.uint16, mode="r")
train_data_dtype = train_data.dtype
train_data_shape = train_data.shape
print(f"data_dtype: {train_data_dtype}, data_shape: {train_data_shape}")
data_dtype: uint16, data_shape: (301966,)
We see that the shape of train data is (301966,), which means that it is a 1D (flattened) array
with \(301966\) elements - this is basically the length of the entire train corpus, in terms of
tokens.
Notation, Context Length, Shuffling and Batching#
However, we are not going to pass the entire training corpus as is to the model.
Instead, we are going to pass a batch of sequences (each sequence of length
context_length) to the model at a time.
Notation#
Let’s consider a sequence \(\mathbf{x} = (x_1, x_2, \ldots, x_T)\), where:
\(x_t\) represents the \(t\)-th token in the sequence,
Each token \(x_t\) is an element of a predefined vocabulary \(\mathcal{V} := \mathcal{X}\),
\(T\) denotes the total number of tokens in the sequence, i.e., the sequence length.
In practice, we handle multiple sequences at once by grouping them into a batch. This batch, denoted as \(\mathcal{B}\), is then presented to the model for parallel processing.
A batch of sequences is represented as a matrix \(\mathbf{X}\), where each row corresponds to a sequence in the batch. If the batch size is \(\mathcal{B}\) and each sequence within the batch has a fixed length \(T\), then \(\mathbf{X}\) can be expressed as:
Here, \(x_{i,j}\) denotes the \(j\)-th token in the \(i\)-th sequence of the batch. It’s important to note that while we represent the sequences in a real-valued space \(\mathbb{Z}^{\mathcal{B} \times T}\) for mathematical convenience, in practice, each \(x_{i,j}\) corresponds to a discrete token from the vocabulary \(\mathcal{X}\) so using \(\mathbb{Z}^{+}\) would be more appropriate.
Context Length / Block Size#
\(T\) is often referred to as the sequence length, or in the context of GPT, it is
the block_size or context_length or max_seq_len.
It is the length of the sequence that the model will be trained on and is also the context length/context window that we often hear about.
For example, Gemini 1.5 was announced to have a standard \(128,000\) token context window, up to a maximum of \(1\) million max length.
Typically, I think that if your model is trained on a certain context length, it is not trivial to change it. For example, if you train a model on a context length of \(128\), you cannot simply change it to \(256\) without retraining the model. But it seems that it is increasingly possible to do so.
Let’s look at an example, if we define our \(L\) to be \(32\), then we would expect each sequence to be of length \(32\).
first_sequence = train_data[0:0+32]
pprint(first_sequence)
first_sequence_decoded = tokenizer.decode(first_sequence)
print(first_sequence_decoded)
memmap([ 5962, 22307, 25, 198, 8421, 356, 5120, 597, 2252, │ │ 11, 3285, 502, 2740, 13, 198, 198, 3237, 25, │ │ 198, 5248, 461, 11, 2740, 13, 198, 198, 5962, │ │ 22307, 25, 198, 1639, 389], dtype=uint16)
First Citizen:
Before we proceed any further, hear me speak.
All:
Speak, speak.
First Citizen:
You are
The example is just extracting \(1\) such sequence \(\mathbf{x}\) from the train corpus. To leverage the prowess of linear algebra operations in CUDA, we would typically pass a batch of sequences \(\mathcal{B}\) to the model at a time.
Furthermore, we would require some level of randomness in the sequences that we pass to the model to enable generalisation. You really do not want the model to overfit to an ordered sequence of tokens in the training corpus.
To this end, let’s see how Karpathy implements batching and shuffling of the sequences.
Shuffling and Discrete Uniform Sampling#
To enable shuffling, Karpathy generates a tensor of random integers (essentially a list of random integers), which serve as indices. These indices are used to select random sequences from the training (and validation) data.
For simplicity, let’s look at the case where batch size is reduced to \(\mathcal{B} = 1\). This means we only need to sample \(1\) sequence from the training data - and consequently we only need \(1\) random index.
We can easily achieve this via torch.randint which generates random integers
from a discrete uniform distribution over the half-open interval \([l, h)\),
and since we only want to sample \(1\) sequence, we set size=(1,).
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
low, high = 0, len(train_data) - composer.block_size
size = (1,)
indices: torch.Tensor = torch.randint(low=low, high=high, size=size, generator=generator)
pprint(indices)
pprint(indices.shape)
tensor([122484])
torch.Size([1])
The mathematical operation performed by torch.randint(low, high, size, generator) can be described as drawing samples from a uniform discrete distribution. Each element of the resulting tensor is an independent and identically distributed [Radford et al., 2019] (i.i.d.) random variable \(X_i\) with the following probability mass function (PMF):
This PMF implies that each integer in the range \([l, h-1]\) has an equal probability of being selected.
In our demonstration, we selected a random index, specifically \(136,016\), from
our training dataset. This serves as a starting point for constructing a
sequence, denoted as \(\mathbf{x}\). This sequence consists of the token found at
the chosen index and extends to include the subsequent \(T\) tokens, where \(T\)
represents the block size. For the sake of simplicity, and to align with our
predefined settings, we have chosen \(T = 8\). This block size is predetermined in
our composer configuration, activated specifically under a debug mode.
In code, we can achieve this by slicing the training data from the random index
to the random index plus the block size. This is done by train_data[random_index:random_index+block_size].
random_sequence = train_data[indices:indices+composer.block_size]
pprint(random_sequence)
pprint(random_sequence.shape)
random_sequence_decoded = tokenizer.decode(random_sequence)
print(tokenizer.decode(random_sequence))
memmap([11503, 290, 21120, 30, 880, 788, 11, 29448], │ dtype=uint16)
(8,)
priest and clerk? well then, amen
One might wonder why the highest value of the random integers is
len(self.train_data) - self.block_size. This is mostly to prevent index out of
range errors. As we shall soon see, we are using these indices to slice a
sequence of length block_size from the data where you start slicing from the
index index and end at index + block_size.
Batching#
Now that we understand how to sample a single sequence from the training data,
let’s look at how we can sample a batch of sequences.
PyTorch made it easy for you, as we can just simply change the size parameter
to (batch_size,) so we can sample \(\mathcal{B}\) number of indices - and
consequently \(\mathcal{B}\) number of sequences.
In our case, if we set \(\mathcal{B} = 2\), we would expect to get \(2\) random indices.
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
low, high = 0, len(train_data) - composer.block_size
size = (composer.batch_size,)
indices: torch.Tensor = torch.randint(low=low, high=high, size=size, generator=generator)
pprint(indices)
pprint(indices.shape)
tensor([122484, 196406])
torch.Size([2])
We then construct a batch of
input sequences \(\mathcal{B}\) by selecting the tokens at the
indices \(122,484\) and \(196,406\) and the next \(T\) tokens via a for loop - and using torch.stack
to stack the sequences into a tensor of shape \(\mathbb{Z}^{\mathcal{B} \times L}\).
So the first row of the batch would be the sequence starting at index \(122,484\) and the second row would be the sequence starting at index \(196,406\), with each sequence having a length of \(T=8\).
x = torch.stack([torch.from_numpy((train_data[index : index + composer.block_size]).astype(np.int64)) for index in indices])
pprint(x)
pprint(x.shape)
tensor([[11503, 290, 21120, 30, 880, 788, 11, 29448], │ │ [ 326, 8616, 373, 14855, 13, 198, 198, 37286]])
torch.Size([2, 8])
It is worth reconciling the fact that the slicing uses [index:index + block_size] and
therefore completes the reasoning behind the len(self.train_data) - self.block_size in
the torch.randint function call - to prevent index out of range errors. Consider
that if we do not subtract block_size from the length of the training data, we might
end up with an index that is the last index of the training data, and when we add
block_size to it, we would end up with an index that is out of range.
Construction of Input and Target Sequences#
As we will define more formally later, GPT model is an autoregressive self-supervised learning model[Lee, 2023] that directly learns a conditional probability distribution \(\mathbb{P}(x_t | x_{<t} ; \Theta)\) over the vocabulary \(\mathcal{V}\) of tokens, which is conditioned on the entire history of tokens \(x_{<t} = (x_1, x_2, \ldots, x_{t-1})\).
We have seen earlier how to construct an input sequence \(\mathbf{x}\) from the training data. To put things into perspective, we consider again the first sequence that we constructed from the training data:
representing the sentence 'priest and clerk? well then, amen'.
Given the autoregressive and self-supervised nature, in order to construct the target sequence \(\mathbf{y}\), we simply shift the input sequence by one token to the left. This means that the target sequence \(\mathbf{y}\) is:
representing the sentence 'and clerk? well then, amen.'. Note here \(13\)
is the index of the next token after the last token in the input sequence.
This behaviour is autoregressive because we are using the context tokens \(x_{<t}\) to predict the next token \(x_t\), and self-supervised because we are using the input sequence \(\mathbf{x}\) to construct the target sequence \(\mathbf{y}\) without any external labels.
To illustrate further, the prediction process during training is cumulative:
For predicting \(x_2\), the model uses \(x_1\) as context: \(\mathbb{P}\left(x_2 \mid x_1\right)\).
For predicting \(x_3\), the model uses both \(x_1\) and \(x_2\) as context: \(\mathbb{P}\left(x_3 \mid x_1, x_2\right)\).
This pattern continues, such that for predicting \(x_t\), the model uses \(x_1, x_2, \ldots, x_{t-1}\) as context: \(\mathbb{P}\left(x_t \mid x_1, x_2, \ldots, x_{t-1}\right)\)
In code, we can achieve this by simply slicing the adding a 1 to the index
in the train_data slicing operation.
y = torch.stack([torch.from_numpy((train_data[index + 1: index + 1 + composer.block_size]).astype(np.int64)) for index in indices])
pprint(y)
pprint(y.shape)
tokenizer.decode(y[0].numpy())
tensor([[ 290, 21120, 30, 880, 788, 11, 29448, 13], │ │ [ 8616, 373, 14855, 13, 198, 198, 37286, 406]])
torch.Size([2, 8])
' and clerk? well then, amen.'
Asynchronous Data Loading and Prefetching#
As we approach the last part of the code, Karpathy moves x and y to the
device and returns them.
if composer.device_type == "cuda":
# pin arrays x,y, which allows us to move them to GPU asynchronously (non_blocking=True)
x, y = x.pin_memory().to(composer.device, non_blocking=True), y.pin_memory().to(composer.device, non_blocking=True)
else:
x, y = x.to(composer.device), y.to(composer.device)
This is a common operation in PyTorch, where we move the data to the underlying device (CPU or GPU or MPS) to leverage the processing capabilities of the device. It goes without saying that modern deep learning models are trained on GPUs - and CUDA is the de facto standard for GPU-accelerated computing.
CUDA allows a pin_memory and non_blocking parameter to be set when transferring
tensor data from CPU to GPU. The pin_memory parameter is used to allow .to("cuda")
to be more performant
as it avoids some implicit CPU-to-CPU copies. Tensors which are pinned in memory
also allow the transfer from CPU to GPU to be done asynchronously via non_blocking with respect to
the host[2].
It can be useful because we can do some other work in CPU while the data is being transferred to GPU. Consider the below scenario:
tensor.pin_memory().to("cuda", non_blocking=True)will transfer the tensor to the GPU asynchronously, and the CPU can continue doing some other work.While waiting, CPU can do some other operations without waiting for the transfer to complete,
Once
tensoris transferred to the GPU, then we can do some other operations on the GPU.
What is worth noting is that CUDA manages the synchronization such that operations on the GPU will not start until the transfer is complete. However, CUDA programming is complex and is out of the scope of this post. Interested readers can see the reference section.
Collating Everything Together#
def get_batch(
composer: Composer,
*,
split: Literal["train", "valid"],
batch_size: int,
block_size: int,
generator: torch.Generator,
device: torch.device,
device_type: Literal["cpu", "cuda"] = "cpu",
) -> Tuple[torch.Tensor, torch.Tensor]:
# We recreate np.memmap every batch to avoid a memory leak, as per
# https://stackoverflow.com/questions/45132940/numpy-memmap-memory-usage-want-to-iterate-once/61472122#61472122
if split == "train":
data = np.memmap(composer.train_path, dtype=np.uint16, mode="r")
else:
data = np.memmap(composer.valid_path, dtype=np.uint16, mode="r")
low, high = 0, len(data) - block_size
size = (batch_size,)
indices = torch.randint(low=low, high=high, size=size, generator=generator)
x = torch.stack([torch.from_numpy((data[index : index + block_size]).astype(np.int64)) for index in indices])
y = torch.stack(
[torch.from_numpy((data[index + 1 : index + 1 + block_size]).astype(np.int64)) for index in indices]
)
if device_type == "cuda":
# pin arrays x,y, which allows us to move them to GPU asynchronously (non_blocking=True)
x, y = x.pin_memory().to(device, non_blocking=True), y.pin_memory().to(device, non_blocking=True)
else:
x, y = x.to(device), y.to(device)
return x, y
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
train_batch = get_batch(composer, split="train", batch_size=composer.batch_size, block_size=composer.block_size, device=composer.device, generator=generator)
x, y = train_batch
pprint(x)
pprint(y)
tensor([[11503, 290, 21120, 30, 880, 788, 11, 29448], │ │ [ 326, 8616, 373, 14855, 13, 198, 198, 37286]])
tensor([[ 290, 21120, 30, 880, 788, 11, 29448, 13], │ │ [ 8616, 373, 14855, 13, 198, 198, 37286, 406]])
Using PyTorch’s Dataset and Dataloader#
It is relatively simple to understand - and since there is not a need to collate the data, which makes things a bit easier.
Generative Pre-trained Transformer (GPT)#
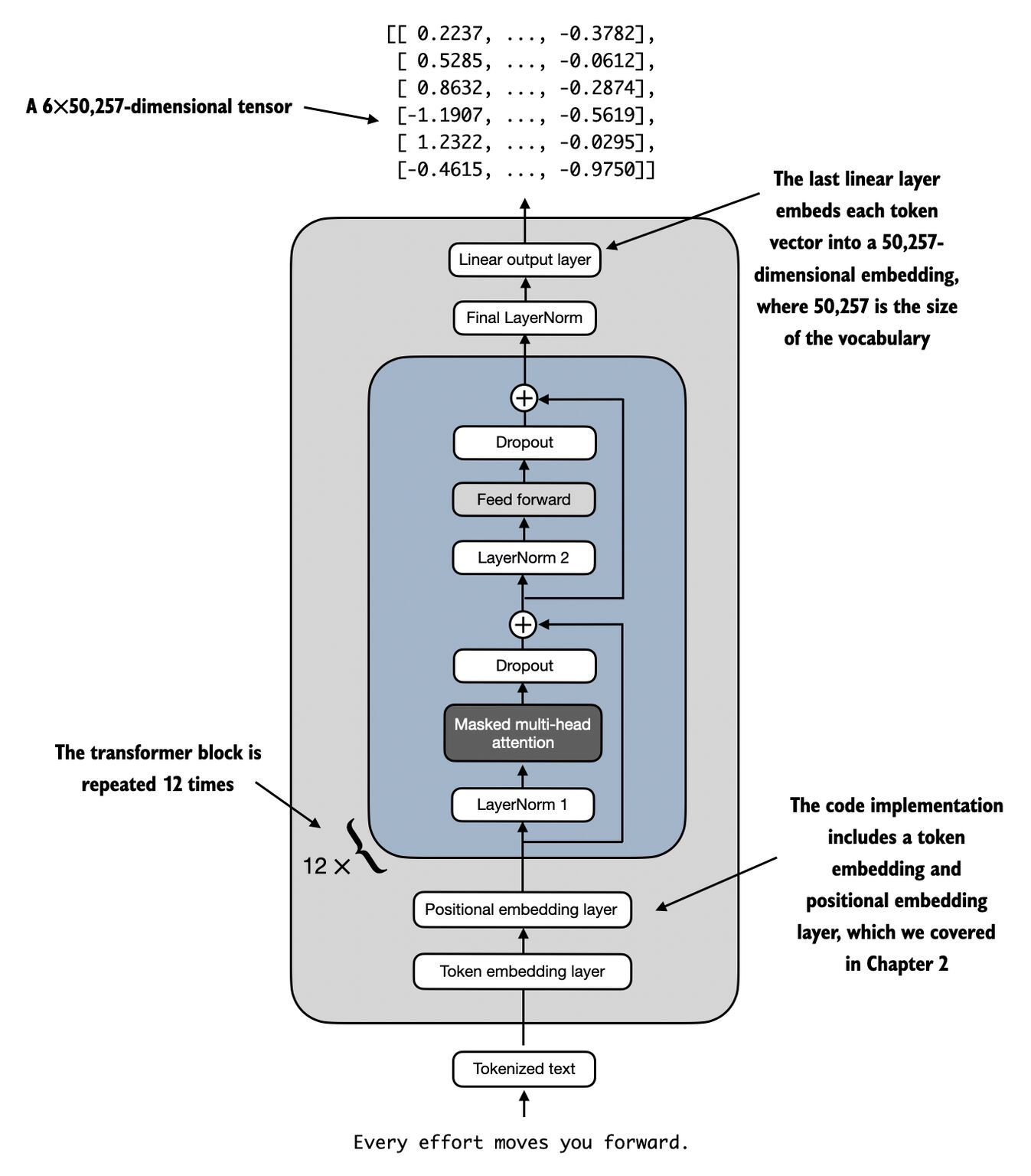
Fig. 2 GPT Architecture. Image Credit: Build a Large Language Model (From Scratch) by Sebastian Raschka#
GPT-2 is a Continuation of GPT-1 with Self-Attention Mechanisms#
The GPT-2 architecture is a transformer-based model, and as the name suggests, it is a continuation of the GPT-1 model with some minor modifications.
GPT-2 utilizes a Transformer architecture [Vaswani et al., 2017] as its backbone, which is distinguished by self-attention mechanisms. This architecture empowers the model to capture complex dependencies and relationships within the data.
Modifications from GPT-1 and Model Stability#
Modifications from GPT-1 include:
Layer normalization is repositioned to the input of each sub-block, mirroring a pre-activation residual network. This modification is believed to offer training stability and model performance. By normalizing the inputs to each sub-block, it is conjectured to alleviate issues tied to internal covariate shift, thus aiding in smoother and potentially faster training.
GPT-2 introduces an additional layer normalization step that is executed after the final self-attention block within the model. This additional normalization step can help ensure that the outputs of the transformer layers are normalized before being passed to subsequent layers or used in further processing, further contributing to model stability.
The GPT-2 paper introduces a modification to the standard weight initialization for the model’s residual layers. Specifically, the weights are scaled by a factor of \(\frac{1}{\sqrt{N_{\text{decoder_blocks}}}}\), where \(N_{\text{decoder_blocks}}\) represents the number of blocks (or layers) in the Transformer’s decoder.
The rationale, as quoted from the paper: “A modified initialization which accounts for the accumulation on the residual path with model depth is used” [Radford et al., 2019], is to ensure that the variance of the input to the block is the same as the variance of the block’s output. This is to ensure that the signal is neither amplified nor diminished as it passes through the block. As the model depth increases, the activations get added/acculumated, and hence the scaling factor is \(\frac{1}{\sqrt{N_{\text{decoder_blocks}}}}\), to scale it down.
Clearly, we can see the empahsis on model stability. In training large language models, numerical stability is paramount; the cost of training is significantly high, with every loss and gradient spike that fails to recover necessitating a return to a previous checkpoint, resulting in substantial GPU hours and potentially tens of thousands of dollars wasted.
The model’s vocabulary is expanded to 50,257 tokens.
The context window size is increased from 512 to 1024 tokens, enhancing the model’s ability to maintain coherence over longer text spans.
A larger batch size of 512, GPT-2 benefits from more stable and effective gradient estimates during training, contributing to improved learning outcomes.
The GPT-2 paper introduces a modification to the standard weight initialization for the model’s residual layers. Specifically, the weights are scaled by a factor of \(\frac{1}{\sqrt{N_{\text{decoder_blocks}}}}\), where \(N_{\text{decoder_blocks}}\) represents the number of blocks (or layers) in the Transformer’s decoder.
The rationale, as quoted from the paper: “A modified initialization which accounts for the accumulation on the residual path with model depth is used” [Radford et al., 2019], is to ensure that the variance of the input to the block is the same as the variance of the block’s output. This is to ensure that the signal is neither amplified nor diminished as it passes through the block. As the model depth increases, the activations get added/acculumated, and hence the scaling factor is \(\frac{1}{\sqrt{N_{\text{decoder_blocks}}}}\), to scale it down.
In practice, seeing how Karpathy implemented it, it seems that the scalings are implemented on the projection layers of the MultiHeadAttention and PositionwiseFFN layers, as seen below:
# apply special scaled init to the residual projections, per GPT-2 paper for pn, p in self.named_parameters(): if pn.endswith('c_proj.weight'): torch.nn.init.normal_(p, mean=0.0, std=0.02/math.sqrt(2 * config.n_layer))
My guess is that the projection layers in both MultiHeadAttention and PositionwiseFFN are critical junctures where the model’s representations are linearly transformed. These layers significantly influence the model’s ability to learn and propagate signals effectively through its depth. Scaling the weights of these projection layers helps to control the rate at which information (and error gradients) is dispersed throughout the network, directly affecting learning stability and efficiency.
I did not implement the custom scaling and just went ahead with default weight scaling:
Weights initialization for the decoder:
def _init_weights(self, module: nn.Module) -> None: normal_init_modules = (nn.Linear, nn.Embedding) if isinstance(module, normal_init_modules): torch.nn.init.normal_(module.weight, mean=0.0, std=0.02) if hasattr(module, "bias") and module.bias is not None: torch.nn.init.zeros_(module.bias)
Weights initialization for the context projection and the context fully connected layers are done using Xavier Uniform initialization.
def _init_weights(self) -> None: """Initialize parameters of the linear layers.""" nn.init.xavier_uniform_(self.ffn["context_fc"].weight) if self.ffn["context_fc"].bias is not None: nn.init.constant_(self.ffn["context_fc"].bias, 0) nn.init.xavier_uniform_(self.ffn["context_projection"].weight) if self.ffn["context_projection"].bias is not None: nn.init.constant_(self.ffn["context_projection"].bias, 0)
GPT-2 Variants#
To this end, we encapsulate some key parameters in Table 4 below, which provides specifications for several GPT-2 variants, distinguished by their scale.
Parameters |
Layers |
d_model |
H |
d_ff |
Activation |
Vocabulary Size |
Context Window |
|---|---|---|---|---|---|---|---|
117M |
12 |
768 |
12 |
3072 |
GELU |
50,257 |
1024 |
345M |
24 |
1024 |
16 |
4096 |
GELU |
50,257 |
1024 |
762M |
36 |
1280 |
20 |
5120 |
GELU |
50,257 |
1024 |
1542M |
48 |
1600 |
25 |
6400 |
GELU |
50,257 |
1024 |
GPT-2 Model Architecture (HuggingFace)#
The below is without the head/softmax layer, from HuggingFace.
from transformers import GPT2Model, GPT2LMHeadModel # type: ignore[import-untyped]
from torchinfo import summary
gpt = GPT2Model.from_pretrained('gpt2')
print(summary(gpt))
print(gpt.config)
======================================================================
Layer (type:depth-idx) Param #
======================================================================
GPT2Model --
├─Embedding: 1-1 38,597,376
├─Embedding: 1-2 786,432
├─Dropout: 1-3 --
├─ModuleList: 1-4 --
│ └─GPT2Block: 2-1 --
│ │ └─LayerNorm: 3-1 1,536
│ │ └─GPT2Attention: 3-2 2,362,368
│ │ └─LayerNorm: 3-3 1,536
│ │ └─GPT2MLP: 3-4 4,722,432
│ └─GPT2Block: 2-2 --
│ │ └─LayerNorm: 3-5 1,536
│ │ └─GPT2Attention: 3-6 2,362,368
│ │ └─LayerNorm: 3-7 1,536
│ │ └─GPT2MLP: 3-8 4,722,432
│ └─GPT2Block: 2-3 --
│ │ └─LayerNorm: 3-9 1,536
│ │ └─GPT2Attention: 3-10 2,362,368
│ │ └─LayerNorm: 3-11 1,536
│ │ └─GPT2MLP: 3-12 4,722,432
│ └─GPT2Block: 2-4 --
│ │ └─LayerNorm: 3-13 1,536
│ │ └─GPT2Attention: 3-14 2,362,368
│ │ └─LayerNorm: 3-15 1,536
│ │ └─GPT2MLP: 3-16 4,722,432
│ └─GPT2Block: 2-5 --
│ │ └─LayerNorm: 3-17 1,536
│ │ └─GPT2Attention: 3-18 2,362,368
│ │ └─LayerNorm: 3-19 1,536
│ │ └─GPT2MLP: 3-20 4,722,432
│ └─GPT2Block: 2-6 --
│ │ └─LayerNorm: 3-21 1,536
│ │ └─GPT2Attention: 3-22 2,362,368
│ │ └─LayerNorm: 3-23 1,536
│ │ └─GPT2MLP: 3-24 4,722,432
│ └─GPT2Block: 2-7 --
│ │ └─LayerNorm: 3-25 1,536
│ │ └─GPT2Attention: 3-26 2,362,368
│ │ └─LayerNorm: 3-27 1,536
│ │ └─GPT2MLP: 3-28 4,722,432
│ └─GPT2Block: 2-8 --
│ │ └─LayerNorm: 3-29 1,536
│ │ └─GPT2Attention: 3-30 2,362,368
│ │ └─LayerNorm: 3-31 1,536
│ │ └─GPT2MLP: 3-32 4,722,432
│ └─GPT2Block: 2-9 --
│ │ └─LayerNorm: 3-33 1,536
│ │ └─GPT2Attention: 3-34 2,362,368
│ │ └─LayerNorm: 3-35 1,536
│ │ └─GPT2MLP: 3-36 4,722,432
│ └─GPT2Block: 2-10 --
│ │ └─LayerNorm: 3-37 1,536
│ │ └─GPT2Attention: 3-38 2,362,368
│ │ └─LayerNorm: 3-39 1,536
│ │ └─GPT2MLP: 3-40 4,722,432
│ └─GPT2Block: 2-11 --
│ │ └─LayerNorm: 3-41 1,536
│ │ └─GPT2Attention: 3-42 2,362,368
│ │ └─LayerNorm: 3-43 1,536
│ │ └─GPT2MLP: 3-44 4,722,432
│ └─GPT2Block: 2-12 --
│ │ └─LayerNorm: 3-45 1,536
│ │ └─GPT2Attention: 3-46 2,362,368
│ │ └─LayerNorm: 3-47 1,536
│ │ └─GPT2MLP: 3-48 4,722,432
├─LayerNorm: 1-5 1,536
======================================================================
Total params: 124,439,808
Trainable params: 124,439,808
Non-trainable params: 0
======================================================================
GPT2Config {
"_name_or_path": "gpt2",
"activation_function": "gelu_new",
"architectures": [
"GPT2LMHeadModel"
],
"attn_pdrop": 0.1,
"bos_token_id": 50256,
"embd_pdrop": 0.1,
"eos_token_id": 50256,
"initializer_range": 0.02,
"layer_norm_epsilon": 1e-05,
"model_type": "gpt2",
"n_ctx": 1024,
"n_embd": 768,
"n_head": 12,
"n_inner": null,
"n_layer": 12,
"n_positions": 1024,
"reorder_and_upcast_attn": false,
"resid_pdrop": 0.1,
"scale_attn_by_inverse_layer_idx": false,
"scale_attn_weights": true,
"summary_activation": null,
"summary_first_dropout": 0.1,
"summary_proj_to_labels": true,
"summary_type": "cls_index",
"summary_use_proj": true,
"task_specific_params": {
"text-generation": {
"do_sample": true,
"max_length": 50
}
},
"transformers_version": "4.38.1",
"use_cache": true,
"vocab_size": 50257
}
# gpt_with_head = GPT2LMHeadModel.from_pretrained('gpt2')
# print(summary(gpt_with_head))
# gpt_medium = GPT2Model.from_pretrained('gpt2-medium')
# print(gpt_medium.config)
# gpt_large = GPT2Model.from_pretrained('gpt2-large')
# print(gpt_large.config)
# gpt_xl = GPT2Model.from_pretrained('gpt2-xl')
# print(gpt_xl.config)
In GPT-2 source code, we can see what the dimension of the feedforward network is. It is defined as:
inner_dim = config.n_inner if config.n_inner is not None else 4 * hidden_size
This is why you do not see it in the config object as if not set, then it is simply
set to 4 * hidden_size.
Token Embeddings#
First, we will look at the first sequence, given by ' priest and clerk? well then, amen',
which we have already mapped to its corresponding token IDs.
The shape is \(1 \times 8\), which is a single sequence of \(8\) tokens. And in this case, we have each word/punctuation mapped to a unique token ID, as seen below.
for token in x[0]:
print(f"Token ID: {token.item()}, Token: {tokenizer.decode([token.item()])}")
Token ID: 11503, Token: priest
Token ID: 290, Token: and
Token ID: 21120, Token: clerk
Token ID: 30, Token: ?
Token ID: 880, Token: well
Token ID: 788, Token: then
Token ID: 11, Token: ,
Token ID: 29448, Token: amen
Next, we need to map each token to a vector (embeddings) in a high-dimensional space.
The integer tokens, by themselves, do not carry much information. For example,
the word priest is tokenized to be 11503, which is an arbitrary integer. In
a one-dimensional Euclidean space, the word priest and the next word and,
indexed by 290, would appear to be very far apart from each other.
However, if we were to change a tokenizer, and somehow the word priest is now
tokenized to be 291, then the words priest and and would appear to be
very near to each other.
This means that the model could potentially learn the relationship of two tokens based solely on their tokenized integers. To address this, we use embedding vectors. While the initial mapping from words to vectors is dependent on the tokenizer and may be arbitrary, during training, the model adjusts these vectors so that words used in similar contexts come to have similar vectors. This allows the model to capture semantic relationships between words - and by extension, allows the model to capture relationships between tokens better.
x0 = x[0]
pprint(tokenizer.decode(x0.cpu().numpy()))
pprint(x0)
' priest and clerk? well then, amen'
tensor([11503, 290, 21120, 30, 880, 788, 11, 29448])
torch.manual_seed(composer.seed)
tok_embed = nn.Embedding(num_embeddings=composer.vocab_size, embedding_dim=composer.d_model)
x0_tok_embed = tok_embed(x0)
pprint(x0_tok_embed)
pprint(x0_tok_embed.shape)
tensor([[-1.0213, 0.3146, -0.2616, 0.3730], │ │ [ 0.5715, 0.1229, -0.8145, -1.4164], │ │ [ 0.4973, -1.1740, -0.6713, -0.1102], │ │ [-2.3167, 0.2943, 0.9573, 0.2935], │ │ [ 0.0623, -0.1054, 0.8182, -2.4184], │ │ [-1.4016, 0.3422, -0.9704, -0.2435], │ │ [-0.0576, -0.0596, 0.2764, -0.2403], │ │ [ 1.2707, -0.5865, -1.4099, -1.3797]], grad_fn=<EmbeddingBackward0>)
torch.Size([8, 4])
Lookup Operation#
So this operation above is essentially a lookup operation, where we look up the
embedding vector for each token in the sequence. This is done by
self.token_embeddings(x). We run it against the first sequence for simplicity,
and x0_tok_embed is the resulting tensor, with a shape of \(T \times D\). In our
case, the sequence length (block size) is \(T = 8\), and the embedding dimension
is \(D = 4\). This means that we have essentially mapped each of the \(8\) tokens
representing priest and clerk? well then, amen to a \(4\)-dimensional vector.
priestis mapped to[-1.0213, 0.3146, -0.2616, 0.3730]andis mapped to[ 0.5715, 0.1229, -0.8145, -1.4164]…
amenis mapped to[ 1.2707, -0.5865, -1.4099, -1.3797]
With each token being a vector, not only does the token carry more information, it is also much easier to do linear algebra operations on the tokens. For example, we can easily calculate the mean/sum of the embeddings for pooling, or we can easily calculate the dot product between two tokens to measure their similarity in a high-dimensional space (as compared to it being an integer with only 1 dimension).
Furthermore, the embeddings are learned during training, and the model would try
to capture semantic relationships between tokens. For example, the model would
try to learn that priest and clerk are related in some way because they
refer to people, and amen is related to priest because it is often used in
religious contexts.
Token Embedding Matrix#
\(\mathbf{W}^{e}\): is the embedding matrix defined as:
where
\(V := \lvert \mathcal{V} \rvert\): is the vocabulary size.
\(D\): is the embedding dimension.
\(e_{j, d}\): is the embedding element at position \(j, d\). For a word \(v_j\) in the vocabulary \(\mathcal{V}\), the corresponding row in \(\mathbf{W}^{e}\) is the embedding vector for that word.
Representation Mapping#
Define a function \(h_{\text{tok_embed}}: \mathcal{V} \to \mathbb{R}^{D}\) such that for each token \(x_t \in \mathcal{V}\), the function \(h_{\text{tok_embed}}(x_t) = \mathbf{W}^{e}_{\text{index}(x_t)}\) returns the embedding vector from \(\mathbf{W}^{e}\), where \(\text{index}(x_t)\) is the index of \(x_t\) in the vocabulary \(\mathcal{V}\) (often times \(x_t\) is already an integer index).
One-Hot Encoding and Embedding Matrix#
It is worth noting that the underlying mechanism of calling tok_embed(x) is
the same as performing a matrix multiplication between a one-hot encoded vector
and the embedding matrix. This is because the one-hot encoded vector is a sparse
vector with only one non-zero element, and when multiplied with the embedding
matrix, it selects the row corresponding to the non-zero element.
x0_ohe = F.one_hot(x0, num_classes=composer.vocab_size)
x0_ohe = x0_ohe.float()
assert x0_ohe.shape == (composer.block_size, composer.vocab_size) # [8, 50257]
for index, token_id in enumerate(x0):
assert x0_ohe[index, token_id].item() == 1.0 # check if the one-hot encoding is correct
Recall our tokenized sequence is
[11503, 290, 21120, 30, 880, 788, 11, 29448].Converting it to one-hot encoding, we would have a matrix of size
[8, 50257](or more generally[B, T, V]in the presence of batch sizeB).Each row is a one-hot vector of the token \(x_{t} \in \mathbb{R}^{V}\) at position \(t\). For example, the first row would be a one-hot vector of the token
11503, so every element in the first row is \(0\) except for the \(11503\)-th element, which is \(1\).A minute quirk here is that the token \(x_{t}\) exists in the continuous space instead of the discrete space. This is because we have to perform the dot product between the one-hot vector and the embedding vector, which is a continuous vector. This is more of a data type coercion. Therefore, in our code, we also converted the one-hot vector to
.float().
embedding_matrix = tok_embed.weight.data
x0_ohe_tok_embed = x0_ohe @ embedding_matrix
torch.testing.assert_close(x0_tok_embed, x0_ohe_tok_embed, rtol=0.0, atol=0.0)
Indeed, we see that the result of tok_embed(x) is the same as the result of
x0_ohe @ embedding_matrix. In other words, you can one hot encoded the input
sequence \(\mathbf{x} = (x_1, x_2, \ldots, x_T)\) and then matrix multiply it with the
embedding matrix \(\mathbf{W}^{e}\) (via a linear layer) to get the same result as tok_embed(x).
\(\mathbf{O}\): one-hot representation of the input sequence \(\mathbf{x} = (x_1, x_2, \ldots, x_T)\). This is a \(T \times V\) matrix, where each row represents a token in the sequence and each column corresponds to a unique word in the vocabulary \(\mathcal{V}\).
\[\begin{split} \begin{aligned} \mathbf{O} &= \begin{bmatrix} o_{1,1} & o_{1,2} & \cdots & o_{1,V} \\ o_{2,1} & o_{2,2} & \cdots & o_{2,V} \\ \vdots & \vdots & \ddots & \vdots \\ o_{T,1} & o_{T,2} & \cdots & o_{T,V} \end{bmatrix} \in \mathbb{R}^{T \times V} \\ &= \begin{bmatrix} \text{---} & \mathbf{o}_{1, :} & \text{---} \\ \text{---} & \mathbf{o}_{2, :} & \text{---} \\ & \vdots & \\ \text{---} & \mathbf{o}_{T, :} & \text{---} \end{bmatrix} \in \mathbb{R}^{T \times V} \end{aligned} \end{split}\]where
\(T\): is the sequence length.
\(V\): is the vocabulary size.
\(o_{t, j}\): is the one-hot encoded element at position \(t, j\). For a given token \(x_t\) at the \(t\)-th position in the sequence \(\mathbf{x}\), if \(f_{\text{stoi}}(x_t)=j\), then the element at position \(j\) in the one-hot vector for token \(x_i\) is 1, and all other elements are 0.
\(\mathbf{o}_{t, :}\): is the one-hot encoded vector for the token \(x_t\) at the \(t\)-th position in the sequence \(\mathbf{x}\). This row form is more important than column form because it serves as the lookup key for the embedding matrix \(\mathbf{W}^{e}\).
\(\mathbf{Z}\): is the output tensor of the embedding layer, obtained by matrix multiplying \(\mathbf{O}\) with \(\mathbf{W}^{e}\), and it is defined as:
\[ \mathbf{Z} = \mathbf{O} \cdot \mathbf{W}^{e} \]\[\begin{split} \begin{aligned} \mathbf{Z} &= \mathbf{O} \cdot \mathbf{W}^{e} \\ &= \begin{bmatrix} z_{1,1} & z_{1,2} & \cdots & z_{1,D} \\ z_{2,1} & z_{2,2} & \cdots & z_{2,D} \\ \vdots & \vdots & \ddots & \vdots \\ z_{T,1} & z_{T,2} & \cdots & z_{T,D} \end{bmatrix} \in \mathbb{R}^{T \times D} \\ &= \begin{bmatrix} \text{---} & \mathbf{z}_{1,:} & \text{---} \\ \text{---} & \mathbf{z}_{2,:} & \text{---} \\ & \vdots & \\ \text{---} & \mathbf{z}_{T,:} & \text{---} \end{bmatrix} \in \mathbb{R}^{T \times D} \end{aligned} \end{split}\]where
\(T\): is the sequence length.
\(D\): is the embedding dimension.
\(z_{t, d}\): is the element at position \(t, d\) in the tensor \(\mathbf{Z}\). For a token \(x_t\) at the \(t\)-th position in the sequence, \(z_{t, :}\) is the \(D\) dimensional embedding vector for that token.
\(\mathbf{z}_{t, :}\): is the \(D\) dimensional embedding vector for the token \(x_t\) at the \(t\)-th position in the sequence.
In this context, each token in the sequence is represented by a \(D\) dimensional vector. So, the output tensor \(\mathbf{Z}\) captures the dense representation of the sequence. Each token in the sequence is replaced by its corresponding embedding vector from the embedding matrix \(\mathbf{W}^{e}\).
As before, the output tensor \(\mathbf{Z}\) carries semantic information about the tokens in the sequence. The closer two vectors are in this embedding space, the more semantically similar they are.
Implementation#
class TokenEmbedding(nn.Module):
def __init__(self, vocab_size: int, d_model: int) -> None:
super().__init__()
self.embedding = nn.Embedding(num_embeddings=vocab_size, embedding_dim=d_model)
def forward(self, x: torch.Tensor) -> torch.Tensor:
return self.embedding(x)
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
tok_embed = TokenEmbedding(vocab_size=composer.vocab_size, d_model=composer.d_model)
W_e = tok_embed.embedding.weight.data
x0 = x0.unsqueeze(dim=0) if x0.ndim == 1 else x0 # [T] -> [B, T]
z0_tok_embed = tok_embed(x0)
assert z0_tok_embed.shape == (1, composer.block_size, composer.d_model) # [B, T, D] = [1, 8, 4]
z0_ohe = F.one_hot(x0, num_classes=composer.vocab_size).float()
assert z0_ohe.shape == (1, composer.block_size, composer.vocab_size) # [T, V] = [8, 50257]
z0_tok_embed_matmul = F.one_hot(x0, num_classes=composer.vocab_size).float() @ W_e
torch.testing.assert_close(z0_tok_embed, z0_tok_embed_matmul, rtol=0.0, atol=0.0, msg="The matrix multiplication is not correct.")
Positional Embeddings#
For the lack of a better phrase, we say that self-attention, the core function of GPTs, is permutation invariant. While it is obvious that the input sequence \(\mathbf{x}\) is ordered in the sense that \(x_1\) comes before \(x_2\), and \(x_2\) comes before \(x_3\), and so on, this information gets lost in the self-attention mechanism. This means that the model does not differentiate “the cat ate the mouse” from “the mouse ate the cat” as long as the tokens are the same - and this is not desirable.
The dominant approach for preserving information about the order of tokens is to represent this to the model as an additional input associated with each token. These inputs are called positional encodings, and they can either be learned or fixed a priori [Zhang et al., 2023]. What this means is that we can either construct a learnable parameter that is updated during training, or we can construct a fixed parameter that is not updated during training. For the sake of completeness, we will discuss briefly the scheme where the positional encodings are fixed a priori based on sinusoidal functions - which is also the scheme described in the paper “Attention is All You Need” [Vaswani et al., 2017].
Definition#
Definition 3 (Positional Encoding)
The positional encoding function \(\mathrm{PE}: \mathbb{N} \times \mathbb{N} \rightarrow \mathbb{R}\) computes the position encoding for each position \(p := t \in \mathbb{N}\) and each dimension \(d = 1, 2, \ldots, D \in \mathbb{N}\) in the input embedding space as follows [Lee, 2023]:
Note that \(10,000\) is an parameter that can be tuned.
Thus, the entire tensor \(\mathbf{P}\) is defined as:
where
\(L\): is the sequence length.
\(D\): is the embedding dimension.
\(p_{i, d}\): is the element at position \(i, d\) in the tensor \(\mathbf{P}\).
Note that \(\mathbf{P}\) is independent of \(\mathbf{Z}\), and it’s computed based on the positional encoding formula used in transformers, which uses sinusoidal functions of different frequencies.
More Intuition on Positional Encodings (Pretty bad analogy, to revise)#
Consider a sentence “Mary visited the museum in Paris.”
The original word embeddings (\(\mathbf{Z}\)) can be thought of as guests at a party, where each guest represents a word: ‘Mary,’ ‘visited,’ ‘the,’ ‘museum,’ ‘in,’ and ‘Paris.’ The personality of each guest represents the semantic meaning of the word they represent.
Now, let’s think of the positional encoding (\(\mathbf{P}\)) as the order in which these guests arrived at the party. This captures the positional information in the sentence. ‘Mary’ was the first to arrive, ‘visited’ the second, and so on.
When we add the positional encoding to the original embeddings (\(\mathbf{Z} = \mathbf{Z} + \mathbf{P}\)), we’re basically combining the personality of each guest (the meaning of the word) with their arrival order at the party (their position in the sentence).
So, for example, ‘Mary’ isn’t just represented as a proper noun referring to a person, but she’s also identified as the first person who arrived at the party. Similarly, ‘Paris’ isn’t just a proper noun referring to a city, but it’s the last entity that arrived.
This way, the combined tensor (\(\mathbf{Z} = \mathbf{Z} + \mathbf{P}\)) captures both the semantic meaning and the positional information for each word, allowing the Transformer to understand both the meaning of the words and their order in the sentence. This is crucial because, in many languages, changing the order of words can drastically alter the meaning of a sentence.
An Example of Positional Encoding#
To demonstrate how positional encodings are calculated for an input sequence
using the given formula, let’s take the first three tokens from the example
sequence ' priest and clerk? well then, amen'. We’ll assume these tokens are
‘priest’, ‘and’, ‘clerk’ and that we’re dealing with an embedding dimension
\(D = 4\) for simplicity. The positions \(p\) of these tokens are 1, 2, and 3,
respectively.
For \(D = 4\), each token’s positional encoding will be a vector of 4 elements. Let’s calculate the positional encodings for \(p = 1, 2, 3\) (corresponding to ‘priest’, ‘and’, ‘clerk?’) and for each dimension \(d = 0, 1, 2, 3\):
Positional Encoding for \(p = 1\) (‘priest’)#
\(d = 0\) (even): \(\sin\left(\frac{1}{10000^{0/4}}\right) = \sin(1)\)
\(d = 1\) (odd): \(\cos\left(\frac{1}{10000^{1/4}}\right) = \cos\left(\frac{1}{\sqrt[4]{10000}}\right)\)
\(d = 2\) (even): \(\sin\left(\frac{1}{10000^{2/4}}\right) = \sin\left(\frac{1}{\sqrt{10000}}\right)\)
\(d = 3\) (odd): \(\cos\left(\frac{1}{10000^{3/4}}\right) = \cos\left(\frac{1}{\sqrt[4]{10000^3}}\right)\)
Positional Encoding for \(p = 2\) (‘and’)#
\(d = 0\) (even): \(\sin\left(\frac{2}{10000^{0/4}}\right) = \sin(2)\)
\(d = 1\) (odd): \(\cos\left(\frac{2}{10000^{1/4}}\right) = \cos\left(\frac{2}{\sqrt[4]{10000}}\right)\)
\(d = 2\) (even): \(\sin\left(\frac{2}{10000^{2/4}}\right) = \sin\left(\frac{2}{\sqrt{10000}}\right)\)
\(d = 3\) (odd): \(\cos\left(\frac{2}{10000^{3/4}}\right) = \cos\left(\frac{2}{\sqrt[4]{10000^3}}\right)\)
Positional Encoding for \(p = 3\) (‘clerk?’)#
\(d = 0\) (even): \(\sin\left(\frac{3}{10000^{0/4}}\right) = \sin(3)\)
\(d = 1\) (odd): \(\cos\left(\frac{3}{10000^{1/4}}\right) = \cos\left(\frac{3}{\sqrt[4]{10000}}\right)\)
\(d = 2\) (even): \(\sin\left(\frac{3}{10000^{2/4}}\right) = \sin\left(\frac{3}{\sqrt{10000}}\right)\)
\(d = 3\) (odd): \(\cos\left(\frac{3}{10000^{3/4}}\right) = \cos\left(\frac{3}{\sqrt[4]{10000^3}}\right)\)
The use of \(10000^{(\cdot/D)}\) with large exponents is designed to provide a wide range of frequencies, enabling the model to distinguish between positions at different scales. In practice, the positional encodings for high-dimensional embeddings (e.g., \(D=512\) in real models) involve very small and precise values, facilitating the model’s learning of complex positional relationships.
Implementation#
from abc import ABC, abstractmethod
import torch
from torch import nn
class PositionalEncoding(ABC, nn.Module):
def __init__(self, d_model: int, context_length: int, dropout: float = 0.0) -> None:
super().__init__()
self.d_model = d_model
self.context_length = context_length
self.dropout = nn.Dropout(p=dropout, inplace=False)
@abstractmethod
def forward(self, x: torch.Tensor) -> torch.Tensor:
...
class Sinusoid(PositionalEncoding):
P: torch.Tensor
def __init__(self, d_model: int, context_length: int, dropout: float = 0.0) -> None:
super().__init__(d_model, context_length, dropout)
P = self._init_positional_encoding()
self.register_buffer("P", P, persistent=True) # with this no need requires_grad=False
def _init_positional_encoding(self) -> torch.Tensor:
"""Initialize the positional encoding tensor."""
P = torch.zeros((1, self.context_length, self.d_model))
position = self._get_position_vector()
div_term = self._get_div_term_vector()
P[:, :, 0::2] = torch.sin(position / div_term)
P[:, :, 1::2] = torch.cos(position / div_term)
return P
def _get_position_vector(self) -> torch.Tensor:
"""Return a vector representing the position of each token in a sequence."""
return torch.arange(self.context_length, dtype=torch.float32).reshape(-1, 1)
def _get_div_term_vector(self) -> torch.Tensor:
"""Return a vector representing the divisor term for positional encoding."""
return torch.pow(
10000,
torch.arange(0, self.d_model, 2, dtype=torch.float32) / self.d_model,
)
def forward(self, z: torch.Tensor) -> torch.Tensor:
z = self._add_positional_encoding(z)
z = self.dropout(z)
return z
def _add_positional_encoding(self, z: torch.Tensor) -> torch.Tensor:
"""Add the positional encoding tensor to the input tensor."""
return z + self.P[:, : z.shape[1], :]
We now do a sum operation between the output of the token embeddings \(\mathbf{Z}\) and the positional encodings \(\mathbf{P}\) to get the final input to the model.
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
pos_embed = Sinusoid(d_model=composer.d_model, context_length=composer.block_size, dropout=0.0)
P = pos_embed.P
z0_tok_embed_with_pos_embed = pos_embed(z0_tok_embed)
z0_tok_embed_add_pos_embed = z0_tok_embed + P
torch.testing.assert_close(z0_tok_embed_with_pos_embed, z0_tok_embed_add_pos_embed, rtol=0.0, atol=0.0) # just to show that adding P to the z0 is the same as pos_embed(z0)
As we have seen earlier using manual calculations, the input sequence’s first token/position at \(t=1\) has values of \([0, 1, 0, 1]\) for the positional encoding with \(D=4\). We simply add this positional encoding to the token embeddings to get the final input embeddings. We can verify it visually below (or can add programmatically).
pprint(P)
pprint(z0_tok_embed)
pprint(z0_tok_embed_with_pos_embed)
tensor([[[ 0.0000, 1.0000, 0.0000, 1.0000], │ │ [ 0.8415, 0.5403, 0.0100, 0.9999], │ │ [ 0.9093, -0.4161, 0.0200, 0.9998], │ │ [ 0.1411, -0.9900, 0.0300, 0.9996], │ │ [-0.7568, -0.6536, 0.0400, 0.9992], │ │ [-0.9589, 0.2837, 0.0500, 0.9988], │ │ [-0.2794, 0.9602, 0.0600, 0.9982], │ │ [ 0.6570, 0.7539, 0.0699, 0.9976]]])
tensor([[[ 0.3077, 0.6799, -0.0569, -0.0053], │ │ [-1.1844, 2.5960, 2.4728, 1.0536], │ │ [-0.8615, 1.1489, 0.5025, -0.7086], │ │ [-0.9848, -0.8165, -2.2122, -0.4416], │ │ [-1.5271, -0.1033, 0.0785, 0.2530], │ │ [-0.9771, -0.6622, -0.2202, -0.8744], │ │ [ 1.5333, 1.7560, 0.5236, 1.2753], │ │ [ 0.5383, -0.1160, 1.8387, -0.7398]]], grad_fn=<EmbeddingBackward0>)
tensor([[[ 0.3077, 1.6799, -0.0569, 0.9947], │ │ [-0.3429, 3.1363, 2.4828, 2.0536], │ │ [ 0.0478, 0.7327, 0.5225, 0.2912], │ │ [-0.8437, -1.8065, -2.1822, 0.5580], │ │ [-2.2839, -0.7569, 0.1185, 1.2522], │ │ [-1.9360, -0.3785, -0.1702, 0.1243], │ │ [ 1.2539, 2.7162, 0.5835, 2.2735], │ │ [ 1.1953, 0.6379, 1.9086, 0.2577]]], grad_fn=<AddBackward0>)
In the forward method of the PositionalEncoding class, the positional
encoding is added to the input X:
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].to(X.device)
return self.dropout(X)
This method slices the precalculated positional encodings tensor self.P to
match the sequence length of X, adds it to X, and then applies dropout. The
result, which is the sum of the original embeddings and the positional
encodings, is returned. So there’s no need to add the positional encodings to
X outside of this class.
So when you call positional_encoding(Z), it adds the positional encodings to
Z and applies dropout, then returns the result. You could store this result in
Z_with_pos_encodings or just overwrite it as Z:
Z = positional_encoding(Z)
Now, Z contains the original embeddings with the positional encodings added
and dropout applied.
In the context of our “hello bot” example, the original tensor Z represented
the word embeddings, where each token in the sequence (i.e., SOS, hello,
bot, EOS) was converted into a 2-dimensional vector capturing the semantic
meaning of each token. After adding positional encoding, the new tensor
represents both the semantic and positional information of each token in the
sequence.
The first row (
[1.1103, -0.6898]) now encapsulates both the meaning of theSOStoken and the information that it’s the first token in the sequence.The second row (
[0.0756, -0.2103]) is now a representation of the wordhellothat carries not just its semantics (e.g., being a greeting), but also the information that it’s the second word in the sentence.The third row (
[2.2618, 0.2702]) likewise carries both the semantics ofbot(likely related to AI or technology), and its position as the third word in the sentence.The last row (
[-0.8478, -0.0320]) encapsulates the semantics ofEOStoken, signifying end of a sentence, and the fact that it’s the last token in the sentence.
The idea here is that in natural language, word order matters. The sentence “hello bot” is not the same as “bot hello” (okay maybe it is the same in this example, a better one is cat eat mouse isn’t the same as mouse eat cat).
So, in a language model, we want our representations to capture not just what words mean, but also where they are in a sentence. Positional encoding is a technique to achieve this goal.
Visualising Positional Encodings#
pos_embed_visual = Sinusoid(d_model=48, context_length=96)
P_visual = pos_embed_visual.P.squeeze().T.cpu().numpy()
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(8, 3))
pos = ax.imshow(P_visual, cmap="RdGy", extent=(1, P_visual.shape[1] + 1, P_visual.shape[0] + 1, 1))
fig.colorbar(pos, ax=ax)
ax.set_xlabel("Position in sequence")
ax.set_ylabel("Hidden dimension")
ax.set_title("Positional encoding over hidden dimensions")
ax.set_xticks([1] + [i * 10 for i in range(1, 1 + P_visual.shape[1] // 10)])
ax.set_yticks([1] + [i * 10 for i in range(1, 1 + P_visual.shape[0] // 10)])
plt.show()
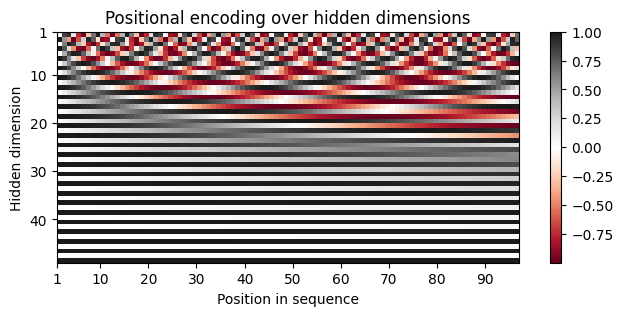
The positional encodings are depicted through sine and cosine functions, each varying in wavelength across the hidden dimensions, to uniquely represent each position. By examining these functions within individual hidden dimensions, we gain deeper insights into the encoding patterns. Here, we present a visualization of the positional encodings across hidden dimensions \(d = 0, 1, 2, 3\) for the initial \(16\) sequence positions [Lippe, 2023].
from typing import List, Tuple
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
def plot_positional_encoding(pe: np.ndarray, block_size: int, figsize: Tuple[int, int] = (12, 4)) -> None:
"""Plot positional encoding for each hidden dimension.
Args:
pe: Positional encoding array.
composer_block_size: Block size of the composer.
figsize: Figure size for the plot.
"""
sns.set_theme()
fig, ax = plt.subplots(2, 2, figsize=figsize)
ax = [a for a_list in ax for a in a_list]
for i, a in enumerate(ax):
a.plot(np.arange(1, block_size + 1), pe[i, :block_size], color=f'C{i}', marker="o", markersize=6, markeredgecolor="black")
a.set_title(f"Encoding in hidden dimension d={i+1}")
a.set_xlabel("Position in sequence", fontsize=10)
a.set_ylabel("Positional encoding", fontsize=10)
a.set_xticks(np.arange(1, 17))
a.tick_params(axis='both', which='major', labelsize=10)
a.tick_params(axis='both', which='minor', labelsize=8)
a.set_ylim(-1.2, 1.2)
fig.subplots_adjust(hspace=0.8)
sns.reset_orig()
plt.show()
plot_positional_encoding(P_visual, 16)
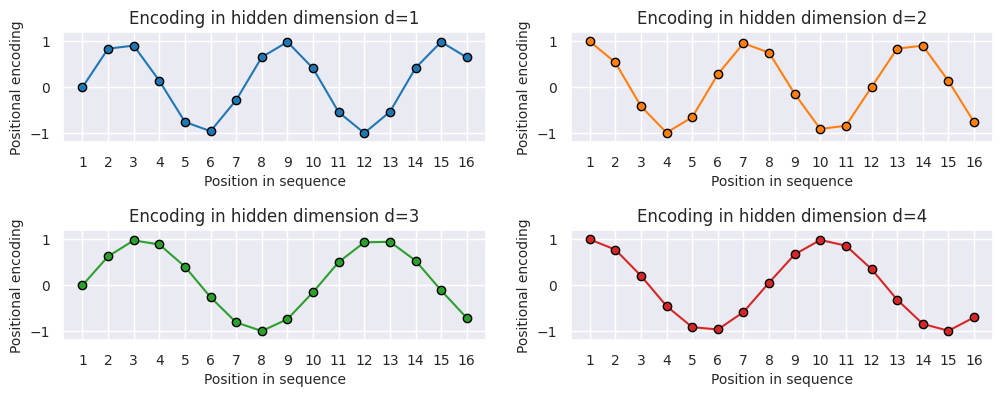
As we can see, the patterns between the hidden dimension 1 and 2 only differ in the starting angle. The wavelength is \(2\pi\) , hence the repetition after position 6 . The hidden dimensions 2 and 3 have about twice the wavelength [Lippe, 2023].
Positional Encodings via Embeddings#
In practice, the positional encodings are learned as part of the GPT-2 [Radford et al., 2019].
So we can replicate the same by using a nn.Embedding layer in PyTorch as in the token embeddings.
\(\mathbf{W}_{p}\) is the positional embedding matrix. Each row of this matrix corresponds to the embedding of a position in a sequence. This matrix is usually of size \(T \times D\), where \(T\) is the maximum length of a sequence we allow in the model, and \(D\) is the dimension of the embedding space.
In other words, the \(\mathbf{P}\) matrix introduced earlier has the same shape as \(\mathbf{W}_{p}\), and while the former is fixed, the latter is learned during the training process.
class PositionalEmbedding(nn.Module):
def __init__(self, d_model: int, context_length: int) -> None:
super().__init__()
self.embedding = nn.Embedding(num_embeddings=context_length, embedding_dim=d_model)
def forward(self, positions: torch.Tensor) -> torch.Tensor:
return self.embedding(positions.to(device=self.embedding.weight.device))
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
pos_embed = PositionalEmbedding(d_model=composer.d_model, context_length=composer.block_size)
positions = torch.arange(start=0, end=composer.block_size, dtype=torch.long) # shape (t)
z0_pos_embed = pos_embed(positions)
z0_tok_embed_with_pos_embed = z0_tok_embed + z0_pos_embed
pprint(z0_tok_embed_with_pos_embed)
tensor([[[-0.9186, 0.6706, 1.4850, -0.4710], │ │ [-0.9049, 2.3350, 3.0957, -0.1025], │ │ [-0.7444, -0.7376, 2.6847, -0.9015], │ │ [-0.4490, -1.7063, -2.5221, 0.3325], │ │ [-1.4034, -2.2840, 0.4485, 0.6674], │ │ [ 0.8796, 1.3154, -0.6523, 0.4923], │ │ [ 2.3765, 1.7139, 2.1815, -0.0332], │ │ [ 1.5345, 0.8230, 3.2535, -0.1055]]], grad_fn=<AddBackward0>)
To this end, we would have wrapped up the first two layers, where we first pass an input sequence \(\mathbf{x}\) through the token embedding layer to obtain the token embeddings \(\mathbf{Z} = \mathbf{W}_{e} \mathbf{x}\), and then add the positional embeddings to the token embeddings to obtain the final embeddings.
The process to encode position into the embeddings is:
Given an input sequence \(\mathbf{x} = \left(x_1, x_2, ..., x_{T}\right)\), where \(x_t\) is the token at position \(t\) in the sequence, we have transformed the input sequence into a sequence of token embeddings \(\mathbf{Z}\), holding both the static semantics and the positional information of the input sequence.
And note this is only for \(1\) sequence, and we can extend this to \(\mathcal{B}\) sequences in a batch.
Layer Normalization#
Definition#
Layer normalization is a technique applied in the context of neural networks to stabilize the learning process by normalizing the inputs across the features for each token in a sequence. Given a data representation \(\mathbf{Z} \in \mathbb{R}^{T \times D}\), where \(T\) is the sequence length (number of tokens) and \(D\) is the hidden dimension (feature space), layer normalization is applied independently to each vector (or token) across the feature dimension \(D\). You can think of each token \(t=1, \ldots, T\) as a separate example, and \(\mathbf{Z}_{t}\) represents each row/token. We then compute the mean and variance for each row/token and then apply the normalization to each row/token. This process is repeated for each row/token in the input matrix \(\mathbf{Z}\).
When considering a batch of such sequences, represented as \(\mathbf{Z}^{\mathcal{B}} \in \mathbb{R}^{\mathcal{B} \times T \times D}\), where \(\mathcal{B}\) is the batch size, layer normalization still focuses on normalizing each token vector within each sequence in the batch. The operation does not aggregate or normalize across different tokens (\(T\) dimension) or different sequences in the batch (\(\mathcal{B}\) dimension); instead, it normalizes the values across the features (\(D\) dimension) for each token.
For a single token \(\mathbf{Z}_t \in \mathbb{R}^{1 \times D}\) in a sequence \(\mathbf{Z} \in \mathbb{R}^{T \times D}\), the the normalization process involves subtracting the mean \(\mu_t\) and dividing by the standard deviation \(\sigma_t\) (adjusted with a small constant \(\epsilon\) for numerical stability) of its features. This process ensures that, for each token, the features are centered around zero with a unit variance.
Definition 4 (Layer Normalization)
Given a token \(\mathbf{Z}_t \in \mathbb{R}^{1 \times D}\) from the sequence \(\mathbf{Z} \in \mathbb{R}^{T \times D}\), the normalized output \(\overline{\mathbf{Z}}_t \in \mathbb{R}^{1 \times D}\) for this token can be expressed as follows:
where:
\(\mathbf{Z}_t\) is the vector of features for the token at position \(t\),
\(\mu_t \in \mathbb{R}\) is the mean of the features for this token,
\(\sigma_t^2 \in \mathbb{R}\) is the variance of the features for this token,
\(\epsilon \in \mathbb{R}\) is a small constant added for numerical stability, ensuring that we never divide by zero or approach zero in the denominator.
The mean \(\mu_t\) and variance \(\sigma_t^2\) are computed as follows:
Here, \(\mathbf{Z}_{td}\) represents the \(d\)-th feature of the token at position \(t\). The division and subtraction are applied element-wise across the feature dimension \(D\) for the token, normalizing each feature based on the statistics of the features within the same token.
Since layer normalization is performed for each token vector across the feature dimension \(D\), the process can be vectorized and applied simultaneously to all \(T\) token vectors in the sequence.
For each token \(t = 1, \ldots, T\), the mean \(\mu_t\) and variance \(\sigma_t^2\) are computed.
Each token vector \(\mathbf{Z}_t\) is then normalized using its respective \(\mu_t\) and \(\sigma_t^2\).
This results in a normalized sequence \(\overline{\mathbf{Z}} \in \mathbb{R}^{T \times D}\), where each token vector \(\overline{\mathbf{Z}}_t\) has been normalized independently. The normalized sequence retains its original shape \((T \times D)\).
When considering a batch of sequences, represented as \(\mathbf{Z}^{\mathcal{B}} \in \mathbb{R}^{\mathcal{B} \times T \times D}\), the layer normalization process extends naturally:
The normalization process is applied independently to each token vector in each sequence within the batch. This means for each sequence \(b\) in the batch \(\mathcal{B}\), and for each token \(t\) in each sequence, the process computes \(\mu_{bt}\) and \(\sigma_{bt}^2\), and normalizes each \(\mathbf{Z}_{bt}\) accordingly.
Since the operation is independent across tokens and sequences, it can be parallelized, allowing for efficient computation over the entire batch.
The result is a batch of normalized sequences, \(\overline{\mathbf{Z}}^{\mathcal{B}} \in \mathbb{R}^{\mathcal{B} \times T \times D}\), where each token vector \(\overline{\mathbf{Z}}_{bt}\) in each sequence of the batch has been normalized based on its own mean and variance.
Broadcasting
It is worth noting that the notation above involves broadcasting, we are essentially subtracting a scalar value (\(\mu_t\)) from a vector (\(\mathbf{Z}_t\)) and dividing by another scalar value (\(\sigma_t\)). This is fine in practice, as the scalar values are broadcasted to match the shape of the vector during the element-wise operations.
We can however make the definition clearer by removing the implicit broadcasting, and say that for each activation \(Z_{td}\) (feature \(d\) of a token at position \(t\)), we compute the normalized activation \(\overline{Z}_{td}\)
where \(\mu_t\) and \(\sigma_t^2\) are computed as before.
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
B, T, D = 2, 3, 4
embedding = torch.randn(B, T, D)
first_sequence_ = embedding[0]
first_sequence_mean = torch.empty_like(first_sequence_)
first_sequence_var = torch.empty_like(first_sequence_)
for index, token in enumerate(first_sequence_):
first_sequence_mean[index, :] = torch.mean(token, dim=-1)
first_sequence_var[index, :] = torch.var(token, dim=-1, unbiased=False)
pprint(first_sequence_mean)
pprint(first_sequence_var)
first_sentence_norm = (first_sequence_ - first_sequence_mean) / torch.sqrt(first_sequence_var)
pprint(first_sentence_norm)
layer_norm = nn.LayerNorm(normalized_shape=D, eps=0)
normalized_embedding = layer_norm(embedding)
pprint(normalized_embedding.shape)
pprint(normalized_embedding)
torch.testing.assert_close(first_sentence_norm, normalized_embedding[0], rtol=1e-5, atol=1e-5)
tensor([[-0.0398, -0.0398, -0.0398, -0.0398], │ │ [-0.1287, -0.1287, -0.1287, -0.1287], │ │ [-0.3987, -0.3987, -0.3987, -0.3987]])
tensor([[1.0230, 1.0230, 1.0230, 1.0230], │ │ [0.4512, 0.4512, 0.4512, 0.4512], │ │ [0.7168, 0.7168, 0.7168, 0.7168]])
tensor([[-1.1730, 0.0302, 1.5639, -0.4210], │ │ [ 0.6077, -0.1970, 1.1190, -1.5296], │ │ [ 1.3132, 0.0139, 0.1715, -1.4986]])
torch.Size([2, 3, 4])
tensor([[[-1.1730, 0.0302, 1.5639, -0.4210], │ │ [ 0.6077, -0.1970, 1.1190, -1.5296], │ │ [ 1.3132, 0.0139, 0.1715, -1.4986]], │ │ │ │ [[-0.3854, 1.6702, -0.9863, -0.2985], │ │ [ 0.3328, -1.2407, -0.5304, 1.4383], │ │ [-0.9720, 0.5154, 1.3870, -0.9305]]], │ grad_fn=<NativeLayerNormBackward0>)
We see that indeed the assertion passed, and our calculations are correct. Note we must
set unbiased=False in the torch.var function to get the same result as the
LayerNorm function because we are using population variance formula.
We can further confirm below now the mean and variance close to 0 and 1 respectively.
mean = torch.mean(normalized_embedding, dim=-1)
std = torch.std(normalized_embedding, dim=-1)
print("\nExample of mean and std for a single sentence across embedding dimensions:")
print("Mean:", mean[0])
print("Standard deviation:", std[0])
Example of mean and std for a single sentence across embedding dimensions:
Mean: tensor([3.7253e-08, 2.9802e-08, 0.0000e+00], grad_fn=<SelectBackward0>)
Standard deviation: tensor([1.1547, 1.1547, 1.1547], grad_fn=<SelectBackward0>)
Learnable Affine Transformation#
Normalizing the activations to have zero mean and unit variance can limit the representational power of the network, and thus after computing the normalized features \(\hat{\mathbf{Z}}_t\) for each token, we introduce a learnable affine transformation (scaling and shifting), in terms of parameters \(\gamma\) and \(\beta\), which are of the same dimensionality as the feature space \(D\), to scale and shift the normalized features, allowing the model to “undo” the normalization if it is beneficial for the learning process.
where \(\overline{\mathbf{Z}}_t\) represents the output of the layer normalization for the token at position \(t\), and \(\odot\) denotes element-wise multiplication. And for each activation \(\mathbf{Z}_{td}\), we have:
where \(\gamma_d\) and \(\beta_d\) are the scaling and shifting parameters for the \(d\)-th feature of the token at position \(t\). However notice that I did not index \(\gamma\) and \(\beta\) by \(t\) because they are shared across all tokens in the sequence.
The notation \(\gamma_{d}\) without indexing \(t\) implies that the scaling parameter \(\gamma\) is feature-specific but shared across all tokens in the sequence. It means that each feature dimension \(d\) across all tokens \(t\) in the sequence has its own unique scaling parameter, but this parameter does not change with different tokens. This is the common setup in layer normalization, where \(\gamma\) and \(\beta\) parameters are learned for each feature dimension \(D\) and are applied identically across all tokens \(T\).
Overall, layer norm is just taking each row in \(\mathbf{Z}\), sum all \(D\) elements in the row, and then calculate the mean and variance. Then, we subtract the mean from each element in the row, divide by the standard deviation, and then scale and shift the result using \(\gamma\) and \(\beta\).
Implementation#
from typing import Optional, Tuple, Union
import torch
from torch import nn
from torch.types import _device, _dtype
class LayerNorm(nn.Module):
__constants__ = ["normalized_shape", "eps", "elementwise_affine"]
normalized_shape: Union[int, Tuple[int, ...]]
eps: float
elementwise_affine: bool
def __init__(
self,
normalized_shape: Union[int, Tuple[int, ...]],
eps: float = 1e-5,
elementwise_affine: bool = True,
device: Optional[Union[_device, str, None]] = None,
dtype: Optional[_dtype] = None,
) -> None:
super().__init__()
factory_kwargs = {"device": device, "dtype": dtype}
if isinstance(normalized_shape, int):
normalized_shape = (normalized_shape,)
self.normalized_shape = normalized_shape
self.eps = eps
self.elementwise_affine = elementwise_affine
if self.elementwise_affine:
self.gamma = nn.Parameter(torch.empty(self.normalized_shape, **factory_kwargs)) # type: ignore[arg-type]
self.beta = nn.Parameter(torch.empty(self.normalized_shape, **factory_kwargs)) # type: ignore[arg-type]
else:
self.register_parameter("gamma", None)
self.register_parameter("beta", None)
self.reset_parameters()
def reset_parameters(self) -> None:
if self.elementwise_affine:
nn.init.ones_(self.gamma)
nn.init.zeros_(self.beta)
def forward(self, x: torch.Tensor) -> torch.Tensor:
mean = x.mean(dim=-1, keepdim=True)
std = x.std(dim=-1, keepdim=True, unbiased=False)
if self.elementwise_affine:
return self.gamma * (x - mean) / (std + self.eps) + self.beta
return (x - mean) / (std + self.eps)
def extra_repr(self) -> str:
return "{normalized_shape}, eps={eps}, elementwise_affine={elementwise_affine}".format(**self.__dict__)
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
ln1 = LayerNorm(normalized_shape=composer.d_model, eps=1e-5, elementwise_affine=True)
z0_tok_embed_with_pos_embed_ln1 = ln1(z0_tok_embed_with_pos_embed)
pprint(z0_tok_embed_with_pos_embed_ln1)
ln1_pytorch = nn.LayerNorm(normalized_shape=composer.d_model, eps=1e-5, elementwise_affine=True)
z0_tok_embed_with_pos_embed_ln1_pytorch = ln1_pytorch(z0_tok_embed_with_pos_embed)
pprint(z0_tok_embed_with_pos_embed_ln1_pytorch)
torch.testing.assert_close(z0_tok_embed_with_pos_embed_ln1, z0_tok_embed_with_pos_embed_ln1_pytorch, rtol=1e-5, atol=1e-5)
tensor([[[-1.1744, 0.5068, 1.3684, -0.7009], │ │ [-1.2140, 0.7421, 1.2014, -0.7295], │ │ [-0.5436, -0.5391, 1.7304, -0.6478], │ │ [ 0.5778, -0.5623, -1.3019, 1.2864], │ │ [-0.6119, -1.3203, 0.8780, 1.0542], │ │ [ 0.5074, 1.1037, -1.5886, -0.0225], │ │ [ 0.8592, 0.1623, 0.6541, -1.6756], │ │ [ 0.1286, -0.4499, 1.5262, -1.2049]]], grad_fn=<AddBackward0>)
tensor([[[-1.1744, 0.5068, 1.3684, -0.7009], │ │ [-1.2140, 0.7421, 1.2014, -0.7295], │ │ [-0.5436, -0.5391, 1.7304, -0.6478], │ │ [ 0.5778, -0.5623, -1.3019, 1.2864], │ │ [-0.6119, -1.3203, 0.8780, 1.0542], │ │ [ 0.5075, 1.1037, -1.5886, -0.0225], │ │ [ 0.8592, 0.1623, 0.6541, -1.6756], │ │ [ 0.1286, -0.4499, 1.5262, -1.2049]]], │ grad_fn=<NativeLayerNormBackward0>)
Layer Norm Stabilises Activation Distributions#
Besides the known fact that layer normalization enables convergence and provdies regularization [Lippe, 2023], it also stabilizes the distributions of activations [Zhang et al., 2023]. Training deep neural networks are challenging, loss can easily be exploded or vanished, and the gradients can be unstable. One simple way is to ensure each layer’s activation has a similar distribution - the intuition is that if each layer’s activation has a similar distribution, then the gradients will also have a similar distribution, and this will stabilize the training process. Layer normalization is one of the techniques that can help to achieve this.
Residual Connection#
I have written a more detailed post on the intuition of ResNet which is heavily adapted from the chapter Residual Networks (ResNet) and ResNeXt from the Dive into Deep Learning book.
For the sake of intuition, we can think of the residual connection as a way to ensure that the original input to a layer is not lost as it passes through the model layers.
Deep neural networks are known to suffer from the vanishing gradient problem, where gradients become increasingly small as they are backpropagated through the layers during training. Since we are backpropagating backwards, the earlier layers are therefore more susceptible to this problem. The weak gradient signal could often be close to \(0\), and this could lead to the model not learning well. Consequently, we mitigate this problem by adding the original input to the output of the layer, so that the gradient signal has a direct path to flow through the network.
Furthermore, Eugene Yan’s blog post Some Intuition on Attention and the Transformer also highlighted that attention acting as a filtering mechanism may block information from passing through, directly resulting flat gradients as a small change to the inputs of the attention layer may not change the outputs that much. Skip (residual) connections help resolve this.
We will see later that Multi-Head Attention mechanism operates on a set of tokens, instead of over a sequence. We encode positional information into the tokens, but there is a risk that the positional information is lost in the multi-head attention layers. The residual connection helps to ensure that the positional information is not lost [Lippe, 2023].
The other well known property of the residual connection is that it helps to learn the identity function. Perhaps the scenario is that the best thing a layer or a series of layer can learn is itself - and we don’t actually want an update.
We quote the following from the Dive into Deep Learning book:
Consider \(\mathcal{F}\), the class of functions that a specific network architecture (together with learning rates and other hyperparameter settings) can reach. That is, for all \(f \in \mathcal{F}\) there exists some set of parameters (e.g., weights and biases) that can be obtained through training on a suitable dataset. Let us assume that \(f^*\) is th “truth” function that we really would like to find. If it is in \(\mathcal{F}\), we are in good shape but typically we will not b quite so lucky. Instead, we will try to find some \(f_{\mathcal{F}}^*\) which is our best bet within \(\mathcal{F}\). For instance, given a dataset with features \(\mathbf{X}\) and labels \(\mathbf{y}\), we might try finding it by solving the following optimization problem:
It is only reasonable to assume that if we design a different and more powerful architecture \(\mathcal{F}^{\prime}\) we should arrive at a better outcome. In other words, we would expect that \(f_{\mathcal{F}}^*\) is “better” than \(f_{\mathcal{F}}^*\). However, if \(\mathcal{F} \nsubseteq \mathcal{F}^{\prime}\) there is no guarantee that this should even happen. In fact, \(f_{\mathcal{F}^{\prime}}^*\) might well be worse.
As illustrated by :numref: fig_functionclasses, for non-nested function classes, a larger function class does not always move closer to the “truth” function \(f^*\). For instance, on the left of :numref: fig_functionclasses, though \(\mathcal{F}_3\) is closer to \(f^*\) than \(\mathcal{F}_1, \mathcal{F}_6\) moves away and there is no guarantee that further increasing the complexity can reduce the distance from \(f^*\). With nested function classes where \(\mathcal{F}_1 \subseteq \ldots \subseteq \mathcal{F}_6\) on the right of :numref: fig_functionclasses, we can avoid the aforementioned issue from the non-nested function classes.
Fig. 3 For non-nested function classes, a larger (indicated by area) function class does not guarantee we will get closer to the “truth” function \(f^*\). This does not happen for nested function classes.#
LayerNorm and Residual Connection#
In our context, we would have the following for GPT-1 and older Transformers:
where the layernorm is applied after the residual connection. In other words,
if Sublayer is a function that represents a sublayer (e.g., MultiHeadAttention),
then in each sub-block of the decoder, we would compute the output and then add
the original input to the output, and then apply layer normalization to the sum.
However, in GPT-2, there is a modification, more concretely, to shift the layer normalization
to the input of the sub-block. This means now instead of applying layer normalization
after the residual connection, we apply it before the residual connection. For example,
if Sublayer is a function that represents a sublayer (e.g., MultiHeadAttention),
then in each sub-block of the decoder, we would first apply layer normalization to the
input, then pass the normalized input to the sublayer, and then add the original input
to the output of the sublayer.
Implementation of Residual Block and AddNorm#
from typing import Callable
import torch
from torch import nn
class ResidualBlock(nn.Module):
def forward(
self,
x: torch.Tensor,
sublayer: Callable[[torch.Tensor], torch.Tensor],
) -> torch.Tensor:
return x + sublayer(x)
class AddNorm(nn.Module):
def __init__(self, feature_dim: int, dropout: float) -> None:
super().__init__()
# fmt: off
self.dropout = nn.Dropout(p=dropout, inplace=False)
self.layer_norm = LayerNorm(normalized_shape=feature_dim, eps=1e-5, elementwise_affine=True)
# fmt: on
def forward(self, x: torch.Tensor, sublayer: Callable[[torch.Tensor], torch.Tensor]) -> torch.Tensor:
"""G(F(x) + x) where G = layer norm and F = sublayer"""
# FIXME: GPT-2 should be x + self.dropout(sublayer(self.layer_norm(x)))
output: torch.Tensor = self.layer_norm(x + sublayer(self.dropout(x)))
return output
Self-Attention#
Intuition of Attention Mechanism#
Attention is not a new concept, and one of the most influencial papers came from Neural Machine Translation by Jointly Learning to Align and Translate [Bahdanau et al., 2014], a paper published during 2014. In the context of our post, we would stick to one intuitive interpretation, that the attention mechanism describes a weighted average of (sequence) elements with the weights dynamically computed based on an input query and elements’ keys [Lippe, 2023]. In other words, we want contextually relevant information to be weighted more heavily than less relevant information. For example, the sentence the cat walks by the river bank would require the word bank to be weighted more heavily than the word the when the word cat is being processed. The dynamic portion is also important because this allows the model to adjust the weights based on an input sequence (note that the learned weights are static but the interaction with the input sequence is dynamic). When attending to the first token cat in the sequence, we would want the token cat to be a weighted average of all the tokens in the sequence, including itself. This is the essence of the self-attention mechanism.
Token Embedding and Vector Representation Process#
Given an input sequence \(\mathbf{x} = \left(x_1, x_2, \ldots, x_T\right)\), where \(T\) is the length of the sequence, and each \(x_t \in \mathcal{V}\) is a token in the sequence, we use a generic embedding function \(h_{\text{emb}}\) to map each token to a vector representation in a continuous vector space:
where \(\mathcal{V}\) is the vocabulary of tokens (discrete space \(\mathbb{Z}\)), and \(D\) is the dimension of the embedding space (continuous space). The output of the embedding function \(h_{\text{emb}}\) is a sequence of vectors \(\mathbf{Z} = \left(\mathbf{z}_1, \mathbf{z}_2, \ldots, \mathbf{z}_T\right)\), where each \(\mathbf{z}_t \in \mathbb{R}^{D}\) is the vector representation of the token \(x_t\) in the sequence. As seen earlier, we represent the sequence of vectors \(\mathbf{Z}\) as a matrix \(\mathbf{Z} \in \mathbb{R}^{T \times D}\), where each row of the matrix represents the vector representation of each token in the sequence.
Queries, Keys, and Values#
Database Analogy#
Let’s draw an analogy to understand the concept of queries, keys, and values in
the context of the attention mechanism. Consider a database \(\mathcal{D}\)
consisting of tuples of keys and values. For instance, the database
\(\mathcal{D}\) might consist of tuples
{("Zhang", "Aston"), ("Lipton", "Zachary"), ("Li", "Mu"), ("Smola", "Alex"), ("Hu", "Rachel"), ("Werness", "Brent")}
with the last name being the key and the first name being the value
[Zhang et al., 2023]. Operations on the database \(\mathcal{D}\) can be performed
using queries \(q\) that operate on the keys and values in the database. More
concretely, if our query is “Li”, or more verbosely, “What is the first name
associated with the last name Li?”, the answer would be “Mu” - the key
associated with the query “What is the first name associated with the last
name Li?” is “Li”, and the value associated with the key “Li” is “Mu”.
Furthermore, if we also allowed for approximate matches, we would retrieve
(“Lipton”, “Zachary”) instead.
More rigorously, we denote \(\mathcal{D} \stackrel{\text { def }}{=}\left\{\left(\mathbf{k}_1, \mathbf{v}_1\right), \ldots\left(\mathbf{k}_m, \mathbf{v}_m\right)\right\}\) a database of \(m\) tuples of keys and values, as well as a query \(\mathbf{q}\). Then we can define the attention over \(\mathcal{D}\) as
where \(\alpha\left(\mathbf{q}, \mathbf{k}_t\right) \in \mathbb{R}(t=1, \ldots, T)\) are scalar attention weights [Zhang et al., 2023]. The operation itself is typically referred to as attention pooling. The term “attention” is used because this operation focuses specifically on those terms that have a substantial weight, denoted as \(\alpha\), meaning it gives more importance to these terms. Consequently, the attention over \(\mathcal{D}\) generates a linear combination of values contained in the database. In fact, this contains the above example as a special case where all but one weight is zero. Why so? Because the query is an exact match for one of the keys.
To illustrate why in the case of an exact match within a database the attention weights (\(\alpha\)) are all zero except for one, let’s use the attention formula provided and consider a simplified example with vectors.
Example 2 (Exact Match Scenario)
Imagine a simplified database \(\mathcal{D}\) consisting of 3 key-value pairs, where each key \(\mathbf{k}_t\) and the query \(\mathbf{q}\) are represented as vectors in some high-dimensional space, and the values \(\mathbf{v}_t\) are also vectors (or can be scalar for simplicity in this example). For simplicity, let’s assume our vectors are in a 2-dimensional space and represent them as follows:
Keys (representing \(3\) keys in the database):
\(\mathbf{k}_1 = [1, 0]\),
\(\mathbf{k}_2 = [0, 1]\),
\(\mathbf{k}_3 = [1, 1]\)
Values (corresponding to the keys):
\(\mathbf{v}_1 = [0.1, 0.9]\),
\(\mathbf{v}_2 = [0.2, 0.8]\),
\(\mathbf{v}_3 = [0.3, 0.7]\)
Query (looking for an item/concept similar to \(\mathbf{k}_1\)):
\(\mathbf{q} = [1, 0]\)
The attention weights \(\alpha(\mathbf{q}, \mathbf{k}_t)\) indicate how similar or relevant each key is to the query. In an exact match scenario, the similarity calculation will result in a high value (e.g., \(1\)) when the query matches a key exactly, and low values (e.g., \(0\)) otherwise. For simplicity, let’s use a simple matching criterion where the weight is \(1\) for an exact match and \(0\) otherwise:
\(\alpha(\mathbf{q}, \mathbf{k}_1) = 1\) (since \(\mathbf{q} = \mathbf{k}_1\), exact match)
\(\alpha(\mathbf{q}, \mathbf{k}_2) = 0\) (since \(\mathbf{q} \neq \mathbf{k}_2\), no match)
\(\alpha(\mathbf{q}, \mathbf{k}_3) = 0\) (since \(\mathbf{q} \neq \mathbf{k}_3\), no match)
Using the attention formula:
This calculation shows that because the attention weights for \(\mathbf{k}_2\) and \(\mathbf{k}_3\) are zero (due to no exact match), they don’t contribute to the final attention output. Only \(\mathbf{k}_1\), which exactly matches the query, has a non-zero weight (1), making it the sole contributor to the attention result. This is a direct consequence of the query being an exact match for one of the keys, leading to a scenario where “all but one weight is zero.”
Queries, Keys, and Values in Attention Mechanism#
The database example is a neat analogy to understand the concept of queries, keys, and values in the context of the attention mechanism. To put things into perspective, each token \(x_t\) in the input sequence \(\mathbf{x}\) emits three vectors through projecting its corresponding token and positional embedding output \(\mathbf{z}_t\), a query vector \(\mathbf{q}_t\), a key vector \(\mathbf{k}_t\), and a value vector \(\mathbf{v}_t\). Consider the earlier example cat walks by the river bank, where each word is a token in the sequence. When we start to process the first token \(\mathbf{z}_1\), cat, we would consider a query vector \(\mathbf{q}_1\), projected from \(\mathbf{z}_1\), to be used to interact with the key vectors \(\mathbf{k}_t\) for \(t \in \{1, 2, \ldots, T\}\), in the sequence - determining how much attention “cat” should pay to every other token in the sequence (including itself). Consequently, it will also emit a key vector \(\mathbf{k}_1\) so that other tokens can interact with it. Subsequently, the attention pooling will form a linear combination of the query vector \(\mathbf{q}_1\) with every other key vector \(\mathbf{k}_t\) in the sequence,
and each \(\alpha(\mathbf{q}_1, \mathbf{k}_t)\) will indicate how much attention the token “cat” should pay to the token at position \(t\) in the sequence. We would later see that we would add a softmax normalization to the attention scores to obtain the final attention weights.
We would then use the attention scores \(\alpha(\mathbf{q}_1, \mathbf{k}_t)\) to create a weighted sum of the value vectors \(\mathbf{v}_t\) to form the new representation of the token “cat”.
Consequently, the first token must also emit a value vector \(\mathbf{v}_1\). You can think of the value vector as carrying the actual information or content that will be aggregated based on the attention scores.
To reiterate, the output \(\operatorname{Attention}(\mathbf{q}_1, \mathbf{k}_t, \mathbf{v}_t)\) will be the new representation of the token “cat” in the sequence, which is a weighted sum of the value vectors \(\mathbf{v}_t\) based on the attention scores \(\alpha(\mathbf{q}_1, \mathbf{k}_t)\) and now not only holds semantic and positional information about the token “cat” itself but also contextual information about the other tokens in the sequence. This allows the token “cat” to have a better understanding of itself in the context of the whole sentence. In this whole input sequence, the most ambiguous token is the token “bank” as it can refer to a financial institution or a river bank. The attention mechanism will help the token “bank” to understand its context in the sentence - likely focusing more on the token “river” than the token “cat” or “walks” to understand its context.
The same process will be repeated for each token in the sequence, where each token will emit a query vector, a key vector, and a value vector. The attention scores will be calculated for each token in the sequence, and the weighted sum of the value vectors will be used to form the new representation of each token in the sequence.
To end this off, we can intuitively think of the query, key and value as follows:
Query: What does the token want to know? Maybe to the token bank, it is trying to figure out if it is a financial institution or a river bank. But obviously, when considering the token “bank” within such an input sequence, the query vector generated for “bank” would not actually ask “Am I a financial institution or a river bank?” but rather would be an abstract feature vector in a \(D\) dimensional subspace that somehow captures the potential and context meanings of the token “bank” and once it is used to interact with the key vectors, it will help to determine later on how much attention the token “bank” should pay to the other tokens in the sequence.
Key: Carrying on from the previous point, if the query vector for the token “bank” is being matched with the key vectors of the other tokens in the sequence, the key “river” will be a good match for the query “bank” as it will help the token “bank” to understand its context in the sentence. In this subspace, the key vector for “river” will be a good match for the query because it is more of an “offering” service to the query vector, and it will know when it is deemed to be important to the query vector. As such, the vectors in this subspace are able to identify itself as important or not based on the query vector.
Value: The value vector is the actual information or content that will be aggregated based on the attention scores. If the attention mechanism determines that “river” is highly relevant to understanding the context of “bank” within the sentence, the value vector associated with “river” will be given more weight in the aggregation process. This means that the characteristics or features encoded in the “river” value vector significantly influence the representation of the sentence or the specific context being analyzed.
Linear Projections#
We have discussed the concept of queries, keys, and values but have not yet discussed how these vectors are obtained. As we have continuously emphasized, the query, key, and value vectors lie in a \(D\)-dimensional subspace, and they encode various abstract information about the tokens in the sequence. Consequently, it is no surprise that these vectors are obtained through linear transformations/projections of the token embeddings \(\mathbf{Z}\) using learned weight matrices \(\mathbf{W}^{\mathbf{Q}}\), \(\mathbf{W}^{\mathbf{K}}\) and \(\mathbf{W}^{\mathbf{V}}\).
Definition 5 (Linear Projections for Queries, Keys, and Values)
In the self-attention mechanism, each token embedding \(\mathbf{z}_t \in \mathbb{R}^{D}\) is projected into a new context vector across different subspaces. This projection is accomplished through three distinct linear transformations, each defined by a unique weight matrix:
where \(d_q, d_k, d_v \in \mathbb{Z}^+\) are the hidden dimensions of the subspaces for the query, key, and value vectors, respectively.
Remark 3 (Dimensionality of the Subspaces)
It is worth noting that this post is written in the context of understand GPT models, and the dimensionality of the query, key, and value vectors are the same and usually equal to the dimensionality of the token embeddings. Thus, we may use \(D\) interchangeably to indicate \(d_k, d_v\) and \(d_q\). This is not always the case, as encoder-decoder models might have different dimensionalities for the query, key, and value vectors. However, query and key must have the same dimensionality for the dot product to work.
Each token embedding \(\mathbf{z}_t\) is transformed into three vectors:
The query vector \(\mathbf{q}_t\), representing what the token is looking for in other parts of the input,
The key vector \(\mathbf{k}_t\), representing how other tokens can be found or matched,
The value vector \(\mathbf{v}_t\), containing the actual information to be used in the output.
These transformations are formally defined as:
with each residing in \(d_q, d_k, d_v\)-dimensional subspaces, respectively.
Given an input sequence of \(T\) tokens, the individual vectors for each token can be stacked into matrices:
where each row of these matrices corresponds to the query, key, and value vectors for each token, respectively.
These matrices are generated through simple matrix multiplication of the token embedding matrix \(\mathbf{Z} \in \mathbb{R}^{T \times D}\) with the weight matrices \(\mathbf{W}^{\mathbf{Q}}, \mathbf{W}^{\mathbf{K}}\) and \(\mathbf{W}^{\mathbf{V}}\):
Scaled Dot-Product Attention#
Definition#
Definition 6 (Scaled Dot-Product Attention)
The attention mechanism is a function that maps a set of queries, keys, and values to an output, all of which are represented as matrices in a \(D\)-dimensional space. Specifically, the function is defined as:
where given a query matrix \(\mathbf{Q} \in \mathbb{R}^{T \times d_q}\), a key matrix \(\mathbf{K} \in \mathbb{R}^{T \times d_k}\), and a value matrix \(\mathbf{V} \in \mathbb{R}^{T \times d_v}\), the attention mechanism computes the the output matrix as follows:
where:
\(\mathbf{Q}\mathbf{K}^{\top}\) represents the dot product between the query and key matrices, resulting in a matrix of scores that indicate the degree of alignment or relevance between each query and all keys.
\(\sqrt{d_k}\) is a scaling factor used to normalize the scores, preventing them from becoming too large and ensuring a stable gradient during training. This scaling factor is particularly important as it helps maintain the softmax output in a numerically stable range [Vaswani et al., 2017].
\(\text{softmax}(\cdot)\) is applied row-wise to convert scores into attention weights, ensuring that for each query, the weights across all keys sum up to 1. This normalization step allows the mechanism to effectively distribute focus across the keys according to their relevance to each query.
The resulting matrix of attention weights is then used to compute a weighted sum of the values in \(\mathbf{V}\), producing the output matrix. This output represents a series of context vectors, each corresponding to a query and containing aggregated information from the most relevant parts of the input sequence as determined by the attention weights.
In what follows, we will break down the components of the attention mechanism and explain how it works in detail:
What is Attention Scoring Function?
Why Softmax?
Why Scale by \(\sqrt{d_k}\)?
What is Context Vector?
Attention Scoring Function#
In order to know which tokens in the sequence are most relevant to the current token, we need to calculate the attention scores between the query and key vectors. Consequently, we would need a scoring function that measures the influence or contribution of the \(j\)-th position on the \(i\)-th position in the sequence. This is achieved through the dot product between the query and key vectors, the reasoning through a Gaussian kernel is rigorous and provides a good intuition why we chose the dot product as the scoring function (other than the fact that it is a measure of similarity).
Definition 7 (Attention Scoring Function)
Define the attention scoring function \(\alpha(\cdot)\) as a function that calculates the relevance or influence of each position \(t\) in the sequence on position \(i\), known as the attention scores. The attention scoring function \(\alpha(\cdot)\) is defined using the dot product between query and key vectors, leveraging its property as a similarity measure.
Specifically, the function is expressed as:
where:
\(\mathbf{q}\) is a query vector representing in the sequence, seeking information or context.
\(\mathbf{k}_t\) is the key vector representing the \(t\)-th position in the sequence, offering context or information.
\(\langle \mathbf{q}, \mathbf{k}_t \rangle\) denotes the dot product between the query vector \(\mathbf{q}\) and the key vector \(\mathbf{k}_t\), which quantifies the level of similarity or alignment between the current position that \(\mathbf{q}\) is at (say \(i\)-th) and \(t\)-th positions in the sequence.
The expression \(\mathbf{q} \cdot \mathbf{k}_t\) is a scalar value that indicates the degree of alignment or relevance between the query at \(i\)-th position and the key at \(t\)-th position in the sequence. We would need to calculate the attention scores for each token in the sequence with respect to the query vector \(\mathbf{q}\), and the key vectors \(\mathbf{k}_t\) for \(t \in \{1, 2, \ldots, T\}\).
So this leads us to:
where
is the matrix of key vectors for each token in the sequence, and the output \(\alpha(\mathbf{q}, \mathbf{K}) \in \mathbb{R}^{1 \times T}\) is a row vector of attention scores for the query vector \(\mathbf{q}\) with respect to each key vector \(\mathbf{k}_t\) for \(t \in \{1, 2, \ldots, T\}\).
Lastly, there are \(T\) such queries in the input sequence \(\mathbf{Q}\), and we can stack all the query vectors \(\mathbf{q}_t\) into a matrix \(\mathbf{Q} \in \mathbb{R}^{T \times d_q}\) to calculate the attention scores for all the queries in the sequence with respect to all the key vectors in the sequence.
To this end, each row of the matrix \(\mathbf{Q}\mathbf{K}^{\top}\) represents the attention scores for each query vector at position \(i\) in the sequence with respect to all the key vectors in the sequence.
Scaling Down the Dot Product of Query and Key Vectors#
Definition 8 (Query and Key are Independent and Identically Distributed (i.i.d.))
Under the assumption of the query \(\mathbf{q}\) and key \(\mathbf{k}_t\) are independent and identically distributed (i.i.d.) random variables with a gaussian distribution of mean \(0\) and variance \(\sigma^2\):
Definition 9 (Variance of Dot Product)
Given that \(\mathbf{q} \overset{\mathrm{iid}}{\sim} \mathcal{N}(0, \sigma^2), \quad \mathbf{k}_t \overset{\mathrm{iid}}{\sim} \mathcal{N}(0, \sigma^2)\), the variance of the dot product between the query vector \(\mathbf{q}\) and the key vector \(\mathbf{k}_t\) is:
Proof. The dot product between \(\mathbf{q}\) and \(\mathbf{k}_t\) can be expressed as the sum of the products of their components:
where \(q_i\) and \(k_{ti}\) are the \(i\)-th components of \(\mathbf{q}\) and \(\mathbf{k}_t\), respectively.
The variance of the sum of random variables (when these variables are independent, which is our case since components are iid) is the sum of their variances. The product \(q_i k_{ti}\) is a new random variable, and its variance can be calculated as follows for a single pair of components:
Given that \(q_i\) and \(k_{ti}\) are independent and both have mean 0:
The expectation of the square of the product is:
Since \(\mathbb{E}[q_i k_{ti}] = 0\), the variance of the product \(q_i k_{ti}\) is simply \(\sigma^4\).
For the dot product, we sum across all \(d_k\) components, and since the variance of the sum of independent random variables is the sum of their variances:
We want to ensure that the variance of the dot product still remains the same as the variance of the query and key vectors at \(\sigma^2\) regardless of the vector dimensions. To do so, we scale down the dot product by \(\sqrt{d_k}\), which is the square root of the dimensionality of the key vectors, this operation would scale the variance of the dot product down by \(\sqrt{d_k}^2 = d_k\) (since variance of a scaled random variable is the square of the scale factor times the original variance).
Now our variance would be \(\sigma^4\) - but it is still not the same as the variance of the query and key vectors. This is okay because the original paper assume the variance \(\sigma^2 = 1\) [Vaswani et al., 2017], and therefore it does not matter since \(\sigma^2 = \sigma^4\) when \(\sigma^2 = 1\).
Definition 10 (Attention Scoring Function with Scaling)
To this end, the updated scoring function is:
Before we look into the reason why we scale down the dot product, let’s first complete the final block of the attention mechanism, which is the softmax normalization.
Softmax#
Definition 11 (Attention Scores)
Currently the attention scores \(\alpha(\mathbf{Q}, \mathbf{K})\) are raw scores that indicate the degree of alignment or relevance between each query and all keys. They can be negative or positive, and they can be large or small. We denote them as the raw attention scores \(\alpha(\mathbf{Q}, \mathbf{K}) \in \mathbb{R}^{T \times T}\).
Definition 12 (Softmax Normalization and Attention Weights)
It is common in deep learning to form a convex combination [Zhang et al., 2023] of the attention scores \(\alpha(\mathbf{Q}, \mathbf{K})\) to obtain the attention weights, denoted as \(\text{softmax}(\alpha(\mathbf{Q}, \mathbf{K}))\), which are non-negative and sum to \(1\). This is achieved through the softmax normalization function, which is defined as:
where:
\(\exp(\cdot)\) is the exponential function, which is applied element-wise to the raw attention scores \(\alpha(\mathbf{Q}, \mathbf{K})\).
The denominator is the sum of the exponentials of the raw attention scores across the \(T\) keys, ensuring that the attention weights sum to \(1\) for each query, allowing the mechanism to effectively distribute focus across the keys according to their relevance to each query.
The choice of softmax is a convenient choice, but not the only choice. However, it is convenient because it is both differentiable, which is often a desirable property for training deep learning models that are optimized using gradient-based methods, and it is also monotonic, which means that the attention weights are preserved exactly in the order as the raw attention scores.
Definition 13 (Attention Scoring Function with Scaling and Softmax)
To this end, our final attention scoring function is:
Context Vector/Matrix#
Consequently, we complete the walkthrough of the scaled dot-product attention mechanism by calculating the context vector, which is the weighted sum of the value vectors based on the attention weights obtained from the softmax normalization.
Definition 14 (Context Vector/Matrix)
Given the attention weights \(\alpha(\mathbf{Q}, \mathbf{K})\) and the value matrix \(\mathbf{V}\), the context vector \(\mathbf{C}\) is defined as the output of the scaled dot-product attention mechanism:
where each row \(\mathbf{c}_t\) of the context matrix \(\mathbf{C}\) is the new embedding of the token at position \(t\) in the sequence, containing not only the semantic and positional information of the token itself, but also contextual information from the other tokens in the sequence.
Numerical Stability and Gradient Saturation#
We can now revisit on the underlying reason why we scale down the dot product \(\mathbf{Q}\mathbf{K}^{\top}\) by \(\sqrt{d_k}\).
First, the softmax function has all the desirable properties we want, smoothness, monotonicity, and differentiability, but it is sensitive to large input values.
The softmax function is defined as follows for a given logit \(z_i\) among a set of logits \(Z\):
If the variance of the logits before applying softmax is too large (not scaled down to a more manageable range), the exponential function \(e^{z_i}\) can lead to extremely large output values for any \(z_i\) that is even slightly larger than others in the set. This is due to the exponential function’s rapid growth with respect to its input value.
Remark 4 (Gradient Saturation)
For one random element: If one of the logits \(z_i\) is significantly larger than the others (which is more likely when the variance of the logits is high), \(e^{z_i}\) will dominate the numerator and denominator of the softmax function for this logit. This will cause the softmax output for this logit to approach 1, as it essentially overshadows all other \(e^{z_j}\) terms in the denominator.
For all others: Simultaneously, the softmax outputs for all other logits \(z_j\) (where \(j \neq i\)) will approach 0, because their \(e^{z_j}\) contributions to the numerator will be negligible compared to \(e^{z_i}\) in the denominator. Thus, the attention mechanism would almost exclusively focus on the token corresponding to the dominant logit, ignoring valuable information from other parts of the input sequence.
Furthermore, the gradients through the softmax function will be very small (close to zero) for all logits except the dominant one, which can lead to gradient saturation and even vanishing gradients during training.
def softmax(z: torch.Tensor) -> torch.Tensor:
return torch.exp(z) / torch.sum(torch.exp(z), axis=0)
# Without scaling: large inputs
logits_large = torch.tensor([10, 20, 30], dtype=torch.float32)
softmax_large = softmax(logits_large)
d_k = 512
scaling_factor = torch.sqrt(torch.tensor(d_k))
scaled_logits = logits_large / scaling_factor
softmax_scaled = softmax(scaled_logits)
print("Softmax without scaling:", softmax_large)
print("Softmax with scaling:", softmax_scaled)
Softmax without scaling: tensor([2.0611e-09, 4.5398e-05, 9.9995e-01])
Softmax with scaling: tensor([0.2010, 0.3126, 0.4864])
As we can see, a vector with large inputs can lead to a sharpening effect on the output of the softmax function, essentially causing the output to be too peaky, converging to 1 for the largest input and 0 for the rest (one-hot).
Remark 5 (Numerical Stability)
We know the importance of weight initialization in deep learning models, this is because it dictates the variance of the activations and gradients throughout the network. Without going into the theory, it is intuitive to think that having similar variance across all layer activations is a desirable property for numerical stability. By doing so, the model helps to ensure that the gradients are stable during backpropagation, avoiding the vanishing or exploding gradients problem and enabling effective learning.
In the specific context of the attention mechanism, the variance of the dot products used to calculate attention scores is scaled down by the factor \(\frac{1}{\sqrt{d_k}}\) to prevent softmax saturation. This allows each element to have a chance to influence the model’s learning, rather than having a single element dominate because of the variance scaling with \(d_k\).
Visualizing Variance of Dot Product#
If we set \(d_k = 512\), and mean \(0\) with unit variance, we will see in action that indeed the scaled dot product has a variance of \(1\) while the unscaled dot product has a variance of \(512\), which coincides with our theoretical analysis.
seed_all(92, True, False)
# Set the dimensionality of the keys and queries
d_k = 512
# Set the batch size, number of heads, and sequence length
B, H, L = 4, 8, 32
# Standard deviation for initialization
sigma = 1.0
# Initialize Q and K with variance sigma^2
Q = torch.randn(B, H, L, d_k) * sigma
K = torch.randn(B, H, L, d_k) * sigma
# Calculate dot products without scaling
unscaled_dot_products = torch.matmul(Q, K.transpose(-2, -1))
# Calculate the variance of the unscaled dot products
unscaled_variance = unscaled_dot_products.var(unbiased=False)
# Apply the scaling factor 1 / sqrt(d_k)
scaled_dot_products = unscaled_dot_products / torch.sqrt(torch.tensor(d_k).float())
# Calculate the variance of the scaled dot products
scaled_variance = scaled_dot_products.var(unbiased=False)
print(f"Unscaled Variance: {unscaled_variance}")
print(f"Scaled Variance: {scaled_variance}")
# Apply softmax to the scaled and unscaled dot products
softmax_unscaled = torch.nn.functional.softmax(unscaled_dot_products, dim=-1)
softmax_scaled = torch.nn.functional.softmax(scaled_dot_products, dim=-1)
Unscaled Variance: 512.0117797851562
Scaled Variance: 1.0000230073928833
Projections Lead to Dynamic Context Vectors#
From the start, we mentioned the attention mechanism describes a weighted average of (sequence) elements with the weights dynamically computed based on an input query and elements’ keys. We can easily see the weighted average part through self-attention. The dynamic part comes from the fact that the context vectors are computed based on the input query and its corresponding keys. There should be no confusion that all the learnable weights in this self-attention mechanism are the weight matrices \(\mathbf{W}^{\mathbf{Q}}\), \(\mathbf{W}^{\mathbf{K}}\) and \(\mathbf{W}^{\mathbf{V}}\), but the dynamic is really because the scoring function uses a dot product \(\mathbf{Q}\mathbf{K}^{\top}\), which is dynamic because it is solely decided by the full input sequence \(\mathbf{x}\). Unlike static embeddings, where the word “cat” will always have the same embedding vector, the context vector for the word “cat” will be different in different sentences because it now depends on the full input sequence \(\mathbf{x}\).
Consequently, the projection of the token embeddings into the query and key space is needed.
Implementation#
class Attention(ABC, nn.Module):
def __init__(self, dropout: float = 0.0) -> None:
super().__init__()
self.dropout = nn.Dropout(p=dropout, inplace=False)
@abstractmethod
def forward(
self,
query: torch.Tensor,
key: torch.Tensor,
value: torch.Tensor,
mask: Optional[torch.BoolTensor] = None,
) -> Tuple[torch.Tensor, torch.Tensor]:
raise NotImplementedError("The `forward` method must be implemented by the subclass.")
class ScaledDotProductAttention(Attention):
def forward(
self,
query: torch.Tensor,
key: torch.Tensor,
value: torch.Tensor,
mask: torch.BoolTensor | None = None,
debug: bool = False,
) -> Tuple[torch.Tensor, torch.Tensor]:
# fmt: off
d_q = query.size(dim=-1)
attention_scores = torch.matmul(query, key.transpose(dim0=-2, dim1=-1)) / torch.sqrt(torch.tensor(d_q).float())
attention_scores = attention_scores.masked_fill(mask == 0, float("-inf")) if mask is not None else attention_scores
attention_weights = attention_scores.softmax(dim=-1)
attention_weights = self.dropout(attention_weights)
context_vector = torch.matmul(attention_weights, value)
# fmt: on
if debug:
return context_vector, attention_weights, attention_scores
return context_vector, attention_weights
torch.manual_seed(42)
B, H, L, D = 4, 8, 32, 512 # batch size, head, context length, embedding dimension
Q = torch.rand(B, H, L, D) # query
K = torch.rand(B, H, L, D) # key
V = torch.rand(B, H, L, D) # value
# Scaled Dot-Product Attention
attention = ScaledDotProductAttention(dropout=0.0)
context_vector, attention_weights = attention(Q, K, V)
assert context_vector.shape == (B, H, L, D)
assert attention_weights.shape == (B, H, L, L)
pprint(context_vector.shape)
pprint(attention_weights.shape)
# assert each row of attention_weights sums to 1
# assert each element of attention_weights is between 0 and 1
attention_weights_summed_over_sequences = attention_weights.sum(dim=-1)
assert torch.allclose(
attention_weights_summed_over_sequences, torch.ones(B, H, L)
), "The attention weights distribution induced by softmax should sum to 1."
assert torch.all(
(0 <= attention_weights) & (attention_weights <= 1)
), "All attention weights should be between 0 and 1."
torch.Size([4, 8, 32, 512])
torch.Size([4, 8, 32, 32])
Heatmap#
def show_attention_heatmaps(
attention_weights: torch.Tensor,
xlabel: str = "Keys",
ylabel: str = "Queries",
show_title: bool = False,
figure_kwargs: Optional[Dict[str, Any]] = None,
plot_kwargs: Optional[Dict[str, Any]] = None,
) -> None:
B, H, _, _ = attention_weights.shape
if isinstance(attention_weights, torch.Tensor):
attention_weights = attention_weights.detach().cpu().numpy()
figure_kwargs = figure_kwargs or {"figsize": (15, 15), "sharex": True, "sharey": True, "squeeze": False}
fig, axes = plt.subplots(B, H, **figure_kwargs)
plot_kwargs = plot_kwargs or {"cmap": "viridis"}
for b, (row_axes, attention_weight) in enumerate(zip(axes, attention_weights)):
for h, (ax, head_attention) in enumerate(zip(row_axes, attention_weight)):
pcm = ax.imshow(head_attention, **plot_kwargs)
if b == B - 1:
ax.set_xlabel(xlabel) # Only the last batch will have the xlabel
if h == 0:
ax.set_ylabel(ylabel) # Only the first head will have the ylabel
if show_title:
ax.set_title(f"Batch {b + 1}, Head {h + 1}")
fig.colorbar(pcm, ax=axes, shrink=0.6)
plt.show()
Connecting back to our earlier database query, the following identity matrix would represent when the query and the key to be an exact match, indicated here naively as if query is 0, then key is also 0, and so on. And thus the weight matrix would have a diagonal of 1s and 0s elsewhere.
attention_weights = torch.eye(10).reshape((1, 1, 10, 10))
show_attention_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
Masked/Causal Self-Attention#
In the context of GPT models, which is a decoder-only architecture, the self-attention mechanism is often referred to as masked self-attention or causal attention. The reason is that the attention mechanism is masked to prevent information flow from future tokens to the current token. Given the autoregressive and self-supervised nature of the GPT models, the prediction for the current token should not be influenced by future tokens, as they are not known during inference.
First, let’s connect to our earlier example of z_0_tok_embed_with_pos_embed to
see the non-masked self-attention mechanism in action.
We would create weights \(\mathbf{W}^{\mathbf{Q}}\), \(\mathbf{W}^{\mathbf{K}}\) and
\(\mathbf{W}^{\mathbf{V}}\) and project the token embeddings into the query, key
and value space. We then pass the query, key and value matrices into the scaled
dot-product attention mechanism to obtain the context matrix \(\mathbf{C}\)
as well as the attention weights \(\alpha(\mathbf{Q}, \mathbf{K})\).
Note since it is for only one sample, we would use lower case
letters instead.
torch.manual_seed(42)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
B, H, T, D = 1, 1, composer.block_size, composer.d_model # batch size, head, context length, embedding dimension
W_q = nn.Linear(in_features=D, out_features=D, bias=False)
W_k = nn.Linear(in_features=D, out_features=D, bias=False)
W_v = nn.Linear(in_features=D, out_features=D, bias=False)
q0 = W_q(z0_tok_embed_with_pos_embed)
k0 = W_k(z0_tok_embed_with_pos_embed)
v0 = W_v(z0_tok_embed_with_pos_embed)
# Scaled Dot-Product Attention
attention = ScaledDotProductAttention(dropout=0.0)
context_vector, attention_weights = attention(q0, k0, v0)
attention_weights = attention_weights.reshape(B, H, T, T)
show_attention_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
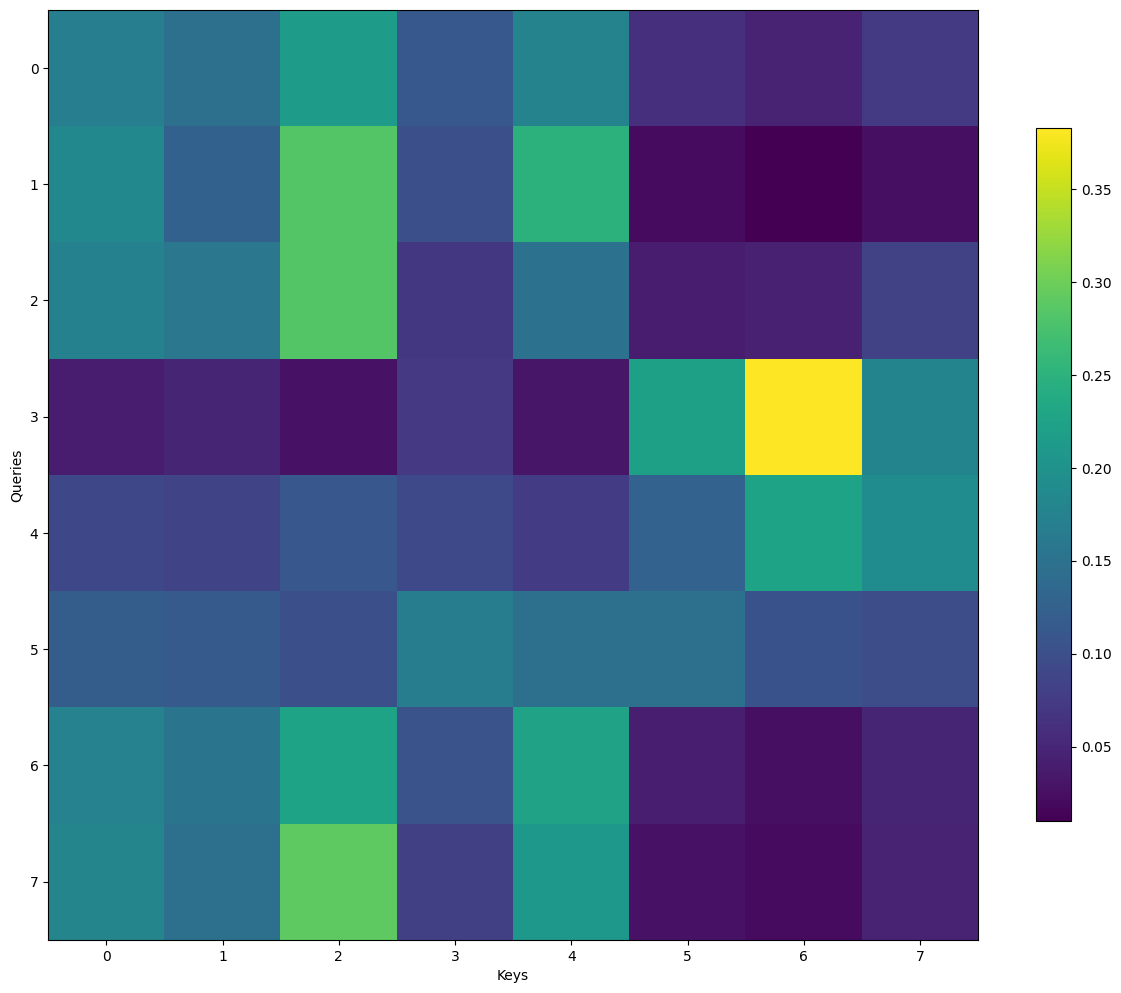
However, there is just one problem. We are allowing the self-attention to attend each token to all other tokens in the sequence, including itself. Since we have \(T\) tokens in the sequence, each sub-sequence \(\mathbf{x}_{1:t}\) would look into the future sub-sequence \(\mathbf{x}_{t+1:T}\), which is trivial now for the model to learn.
Naive Way To Handle Future Mask
Naively, we can dissect the input sequence \(\mathbf{x}\) into \(T\) sub-sequences, and run the self-attention \(T\) times independently. This means we are really treating one sequence as \(T\) sub-samples. But this is inefficient.
To fix this, we introduce a mask, where the mask effectively zeros out the attention scores for the future tokens in the sequence. This would result in the usage of an upper-triangular matrix for the attention scores, and the softmax would then zero out the future tokens in the sequence.
torch.manual_seed(42)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
B, H, T, D = 1, 1, composer.block_size, composer.d_model # batch size, head, context length, embedding dimension
W_q = nn.Linear(in_features=D, out_features=D, bias=False)
W_k = nn.Linear(in_features=D, out_features=D, bias=False)
W_v = nn.Linear(in_features=D, out_features=D, bias=False)
q0 = W_q(z0_tok_embed_with_pos_embed)
k0 = W_k(z0_tok_embed_with_pos_embed)
v0 = W_v(z0_tok_embed_with_pos_embed)
tril_mask = torch.tril(torch.ones((T, T), dtype=torch.bool))
pprint(tril_mask)
# Scaled Dot-Product Attention
attention = ScaledDotProductAttention(dropout=0.0)
context_vector, attention_weights, attention_scores = attention(q0, k0, v0, mask=tril_mask, debug=True)
pprint(attention_scores.squeeze(0).squeeze(0))
pprint(attention_weights)
attention_weights = attention_weights.reshape(B, H, T, T)
show_attention_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries')
tensor([[ True, False, False, False, False, False, False, False], │ │ [ True, True, False, False, False, False, False, False], │ │ [ True, True, True, False, False, False, False, False], │ │ [ True, True, True, True, False, False, False, False], │ │ [ True, True, True, True, True, False, False, False], │ │ [ True, True, True, True, True, True, False, False], │ │ [ True, True, True, True, True, True, True, False], │ │ [ True, True, True, True, True, True, True, True]])
tensor([[ 0.4721, -inf, -inf, -inf, -inf, -inf, -inf, -inf], │ │ [ 0.9305, 0.5463, -inf, -inf, -inf, -inf, -inf, -inf], │ │ [ 0.6937, 0.6022, 1.1826, -inf, -inf, -inf, -inf, -inf], │ │ [-0.7824, -0.5645, -1.1218, -0.1659, -inf, -inf, -inf, -inf], │ │ [-0.2023, -0.2518, -0.0057, -0.1813, -0.3737, -inf, -inf, -inf], │ │ [-0.1110, -0.1470, -0.2887, 0.2175, 0.0896, 0.0917, -inf, -inf], │ │ [ 0.6619, 0.5281, 0.9173, 0.1447, 0.9101, -0.7911, -1.2993, -inf], │ │ [ 0.8410, 0.6451, 1.3262, 0.0369, 0.9972, -1.0329, -1.3433, -0.5124]], │ grad_fn=<SqueezeBackward1>)
tensor([[[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], │ │ [0.5949, 0.4051, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], │ │ [0.2822, 0.2576, 0.4602, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000], │ │ [0.2080, 0.2586, 0.1481, 0.3853, 0.0000, 0.0000, 0.0000, 0.0000], │ │ [0.1987, 0.1891, 0.2419, 0.2029, 0.1674, 0.0000, 0.0000, 0.0000], │ │ [0.1507, 0.1453, 0.1261, 0.2092, 0.1841, 0.1845, 0.0000, 0.0000], │ │ [0.1846, 0.1614, 0.2383, 0.1100, 0.2366, 0.0432, 0.0260, 0.0000], │ │ [0.1790, 0.1471, 0.2907, 0.0801, 0.2092, 0.0275, 0.0201, 0.0462]]], │ grad_fn=<SoftmaxBackward0>)
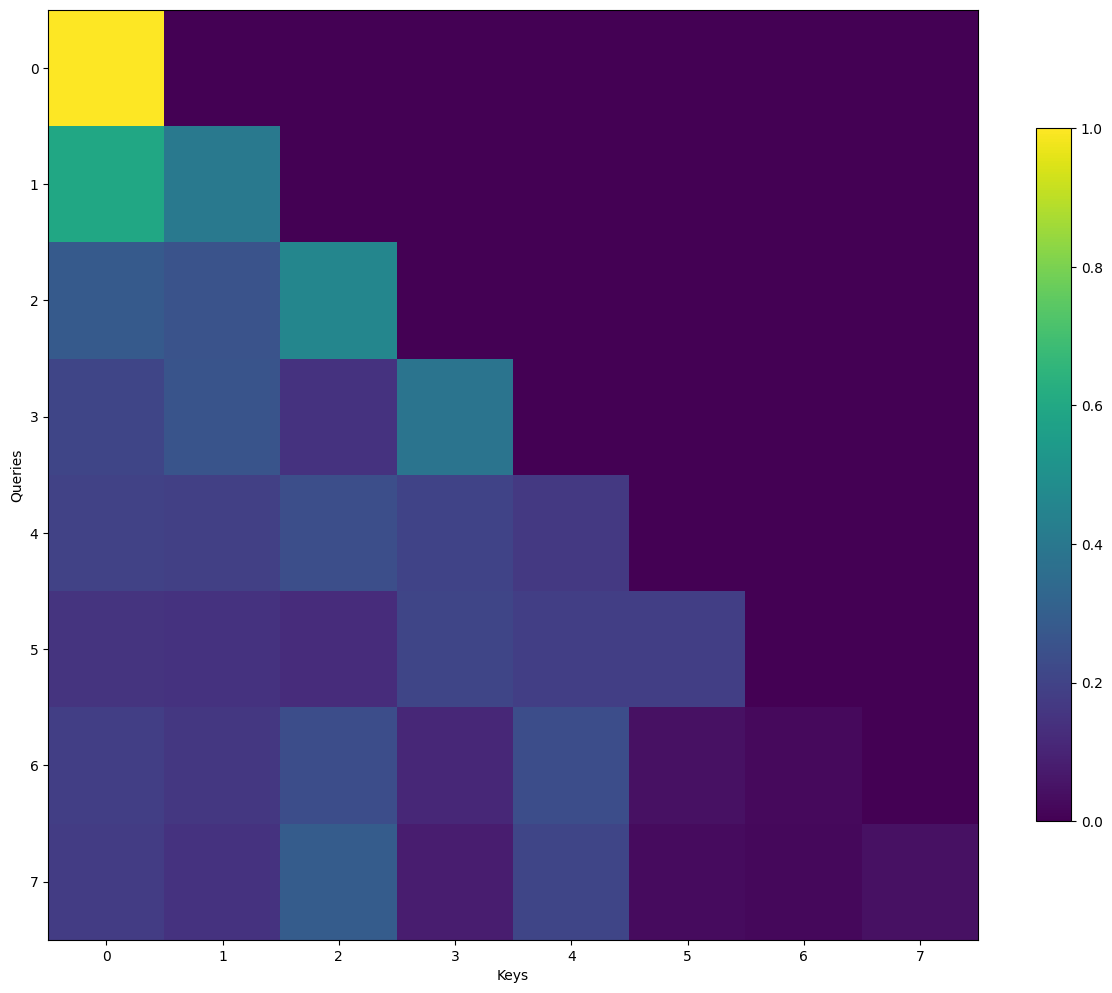
x0_decoded = tokenizer.decode(x0.squeeze().detach().cpu().numpy())
pprint(x0_decoded)
' priest and clerk? well then, amen'
From the print logs and plots above, it is pretty clear how for one sequence,
the future mask is working. Consider our decoded first sample
priest and clerk? well then, amen. The result of \(\mathbf{Q}\mathbf{K}^{\top}\)
would be a matrix of attention weights of size \(T \times T\). As we mentioned
earlier, if we do not mask, then for instance, the second row being the token
and would have information on every token, including clerk, amen etc. This
is considered leakage of information.
So when we provide such a triangular mask:
and apply it to the attention scores, we would see that the attention scores would have \(-\infty\) for the future tokens,
and lastly applying the softmax function, we would see that the future tokens
would have a softmax output of \(0\), a neat trick to ask the loss function to not
consider the future tokens in the sequence. We can even use ignore_index in
PyTorch’s loss function like nn.CrossEntropyLoss to ignore the future tokens
via a given mask index.
Last Token has Full Context#
And finally, the context_vector is a matrix of size \(T \times d_v\) where each
row is the context vector for each token in the sequence, containing not only
the semantic and positional information of the token itself, but also contextual
information from the preceding tokens in the sequence.
For example:
The first token
priestwould have a context vector that contains information from the tokenpriestitself.The second token
andwould have a context vector that contains information from the tokenpriestandand.The third token
clerkwould have a context vector that contains information from the tokenpriest,andandclerk.…
The last token
amenwould have a context vector that contains information from the tokenpriest,and,clerk, …,amen.
As a consequence, the last token would be the only token that has the full context of the sequence, and this is why while generating text, we would only need to use the context vector of the last token to generate the next token.
To this end, each sequence \(\mathbf{x}\) is transformed to a \(T \times d_v\)
It is worth noting that one can connect back to the theory earlier on how one sequence \(\mathbf{x}\) is decomposed to a \(T \times d_v\) matrix where \(d_v = D\) when only one head is involved. The difference is huge because each row of the embedding \(\mathbf{z}\) before passing through attention would only hold that single token \(x_t\)’s semantic and positional info without notion of any other tokens in the sequence. Now, each row of the context vector \(\mathbf{c}_t\) would hold the semantic and positional info of the token \(x_t\) as well as the context information from the preceding tokens in the sequence.
Lastly, each sequence can be thought of having \(T\) sub-samples, this is in line with our objective to model the joint distribution of one sequence \(\mathbf{x}\) - which is decomposed into \(T\) conditional probability.
Computational Complexity of Self-Attention#
It is easy to see that computing the dot product in self-attention quadratic over its sequence length \(T\). And naively, we would require \(\mathcal{O}(T^2 \cdot D)\) time to compute the self-attention on a sequence of length \(T\) and \(D\)-dimensional representations. We see a table listed below, referenced from the paper Attention is All You Need [Vaswani et al., 2017], with complexity per layer, the number of sequential operations, and maximum path length. The complexity is measured by the upper bound of the number of operations to perform, while the maximum path length represents the maximum number of steps a forward or backward signal has to traverse to reach any other position. The lower this length, the better gradient signals can backpropagate for long-range dependencies [Lippe, 2023].
Layer Type |
Complexity per Layer |
Sequential Operations |
Maximum Path Length |
|---|---|---|---|
Self-Attention |
\(\mathcal{O}(T^2 \cdot D)\) |
\(\mathcal{O}(1)\) |
\(\mathcal{O}(1)\) |
Recurrent |
\(\mathcal{O}(T \cdot D^2)\) |
\(\mathcal{O}(T)\) |
\(\mathcal{O}(T)\) |
Convolutional |
\(\mathcal{O}(K \cdot T \cdot D^2)\) |
\(\mathcal{O}(1)\) |
\(\mathcal{O}(\log_K(T))\) |
Self-Attention (restricted) |
\(\mathcal{O}(R \cdot T \cdot D)\) |
\(\mathcal{O}(1)\) |
\(\mathcal{O}\left(\frac{T}{R}\right)\) |
In the table, we have:
\(T\) is the sequence length,
\(D\) is the representation dimension,
\(K\) is the kernel size of the convolution,
\(R\) is the size of the neighborhood in restricted self-attention.
It is not easy to see that the parallel computation of self-attention is favourable, why so? Because unlike recurrent, where we need to strictly follow the sequence, in self-attention, we simultaneously compute the attention scores for all pairs of positions. This is why the maximum path length is \(\mathcal{O}(1)\) for self-attention, since the minimum number of processing steps required to propagate information from any input position to any other position is a constant, regardless of the sequence length, within the same layer, whereas for recurrent, it is \(\mathcal{O}(T)\) because information from the first token in the sequence needs to pass through all the tokens to reach the last token. It is worth noting that when \(T >> D\), self-attention is more computationally expensive than RNNs.
Self-Attention Enables Parallelism#
RNNs process data sequences in a serial manner, meaning they handle one element of the sequence at a time in a step-wise fashion. This sequential processing is due to the RNN’s architecture, which relies on the previous step’s hidden state to compute the current step’s output. Because each step depends on the outcome of the previous step, RNNs inherently have a difficult time leveraging parallel computation within a sequence. The computational complexity of processing a sequence is therefore \(\mathcal{O}(T)\), as the model must iterate through each element of the sequence one after the other.
GPT and other transformer-based models, on the other hand, use a different approach that allows for much more parallelization. Transformers process entire sequences of data at once, rather than step-by-step. This is possible due to the attention mechanism, which computes relationships between all elements in a sequence in parallel and hence the computational complexity of processing a sequence is \(\mathcal{O}(1)\) - irrespective of the sequence length \(T\).
Complexity per Layer#
Essentialy, this refers to the total computational complexity for processing a layer given an input sequence of length \(T\) and model dimension \(D\). For self-attention, this is \(\mathcal{O}(T^2 \cdot D)\), indicating the complexity grows quadratically with the length of the input sequence and linearly with the dimension of the model. This is due to the pairwise interactions between elements in the sequence.
Sequential Operations#
This column refers to the depth of sequential operations that cannot be parallelized. For self-attention, it’s marked as \(\mathcal{O}(1)\), meaning that, in terms of depth of operations that must be executed sequentially (one after the other), self-attention does not increase with the sequence length. This is because, despite the quadratic computational complexity in terms of total operations (\(\mathcal{O}(T^2 \cdot D)\)), the attention computation is essentially computed via matrix multiplication in one go.
Maximum Path Length#
This refers to the longest distance information must travel in the network from input to output. For self-attention, this is also \(\mathcal{O}(1)\), indicating that any output unit can directly attend to any input unit without intermediate steps. This contrasts with RNNs, where the path length can grow linearly with the sequence length (\(\mathcal{O}(T)\)).
The \(\mathcal{O}(1)\) in the “Sequential Operations” and “Maximum Path Length” columns for self-attention highlights its parallelization advantage and direct information flow capability. It does not, however, denote the overall computational complexity of processing a layer, which remains \(\mathcal{O}(T^2 \cdot D)\) due to the pairwise attention computations.
More Intuition in Andrej Karpathy’s Video
There’s much more intuition in Andrej Karpathy’s video on the Let’s Build GPT: from scratch, in code, spelled out. He mentions things like:
Averaging past context with for loops, the weakest for of aggregation.
Matrix multiply as weighted aggregation.
Adding softmax to make it a weighted average.
Attention as communication.
Attention has no notion of space and operates over sets.
There is no communication across batch dimension.
This blog post implements what Andrej mentioned in the video.
Multi-Head Attention#
In practice, given the same set of queries, keys, and values we may want our model to combine knowledge from different behaviors of the same attention mechanism, such as capturing dependencies of various ranges (e.g., shorter-range vs. longer-range) within a sequence. Thus, it may be beneficial to allow our attention mechanism to jointly use different representation subspaces of queries, keys, and values [Zhang et al., 2023].
What this implies is that the natural language is a complex space, and as highlighted in the book Speech and Language Processing by Jurafsky and Martin, there are distinct semantic, syntactic and discourse relationships that can hold between words in a sentence. For example, the verb “ate” in the sentence “The cat ate the mouse” has a semantic relationship with the noun “cat” and “mouse”, and a syntactic relationship with the noun “the”. It would be difficult for a single head to hold all such representations over just a singled weighted average, and this is where multi-head attention comes in.
Multi-head attention is a mechanism that allows the model to jointly attend to information from different representation subspaces at different positions.
Intuition#
Eugene Yan’s article Some Intuition on Attention and the Transformer provides good intuition on multi-head attention. We use his sample sequence “The chicken crossed the road carelessly” to illustrate the intuition.
One head might specifically capture the action-subject relationship, linking “crossed” with “chicken.”
Another head could focus on the action-object relationship, associating “crossed” with “road.”
Yet another head might explore the manner in which the action is performed, connecting “crossed” with “carelessly.”
Definition#
The multi-head attention is a function that maps a query matrix \(\mathbf{Q} \in \mathbb{R}^{T \times d_q}\), a key matrix \(\mathbf{K} \in \mathbb{R}^{T \times d_k}\), and a value matrix \(\mathbf{V} \in \mathbb{R}^{T \times d_v}\) to an output matrix defined as \(\text{MultiHead}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) \in \mathbb{R}^{T \times d_v}\). The function is defined as:
where each \(\text{head}_h\) is the context vector \(\mathbf{C}_h\) obtained from the \(h\)-th head of the self-attention mechanism. The \(\oplus\) operator denotes the concatenation operation that concatenates the context vectors \(\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_H\) along the feature dimension, which essentially still result in the dimension \(T \times D\). The \(\mathbf{W}^O\) is a learnable weight matrix that projects the concatenated context vectors back to the original dimensionality \(D\).
Some other notations:
\(H\) is the number of attention heads, which is a hyperparameter of the multi-head attention mechanism.
\(\mathbf{W}_{h}^{\mathbf{Q}} \in \mathbb{R}^{D \times d_q}\): The learnable query weight matrix for the \(h\)-th head.
Note that \(d_q = \frac{D}{H}\), where \(D\) is the hidden dimension of the token embeddings.
\(\mathbf{W}_{h}^{\mathbf{K}} \in \mathbb{R}^{D \times d_k}\): The key weight matrix for the \(h\)-th head.
Note that \(d_k = \frac{D}{H}\), where \(D\) is the hidden dimension of the token embeddings.
\(\mathbf{W}_{h}^{\mathbf{V}} \in \mathbb{R}^{D \times d_v}\): The value weight matrix for the \(h\)-th head.
Note that \(d_v = \frac{D}{H}\), where \(D\) is the hidden dimension of the token embeddings.
\(\mathbf{Q}_h\), \(\mathbf{K}_h\), and \(\mathbf{V}_h\) are the query, key, and value matrices for the \(h\)-th head, respectively.
\(\text{head}_h = \text{Attention}(\mathbf{Q}_h, \mathbf{K}_h, \mathbf{V}_h)\) is the context vector \(\mathbf{C}_h\) obtained from the \(h\)-th head of the self-attention mechanism.
\(\oplus\) is just \(\text{Concat}(\cdot)\), the concatenation operation that concatenates the head/context matrices \(\mathbf{C}_1, \mathbf{C}_2, \ldots, \mathbf{C}_H\) along the feature dimension, resulting in a matrix of context vectors of shape \(\mathbb{R}^{T \times H \cdot d_v} = \mathbb{R}^{T \times D}\).
\(\mathbf{W}^O \in \mathbb{R}^{d_v \times H \cdot d_v}\) is a learnable weight matrix that projects the concatenated context vectors back to the original dimensionality \(D\).
Without the batch dimension \(\mathcal{B}\), the output matrix \(\mathbf{A}\) is of shape \(\mathbb{R}^{T \times D}\), where each row \(\mathbf{a}_t\) of the output matrix \(\mathbf{A}\) is the new embedding of the token at position \(t\) in the sequence, containing not only the semantic and positional information of the token itself, but also contextual information from the other tokens in the sequence.
Implementation#
class MultiHeadedAttention(nn.Module):
__slots__ = [
"d_model",
"d_k",
"d_q",
"d_v",
"H",
"W_Q",
"W_K",
"W_V",
"W_O",
"attention",
"dropout",
"context_vector",
"attention_weights",
]
def __init__(
self,
attention: Attention,
H: int,
d_model: int,
dropout: float = 0.1,
bias: bool = False,
) -> None:
super().__init__()
assert d_model % H == 0, "The number of heads must divide the embedding dimension."
# fmt: off
self.d_model = d_model # D
self.d_k = d_model // H # stay true to notations
self.d_q = d_model // H
self.d_v = d_model // H
self.H = H # number of heads
# shadow my notations, actually they are of shape D x D.
self.W_Q = nn.Linear(self.d_model, self.d_q * self.H, bias=bias) # D x D
self.W_K = nn.Linear(self.d_model, self.d_k * self.H, bias=bias)
self.W_V = nn.Linear(self.d_model, self.d_v * self.H, bias=bias)
self.W_O = nn.Linear(self.d_model, self.d_model, bias=bias)
self.attention = attention
self.dropout = nn.Dropout(p=dropout, inplace=False)
self.context_vector: torch.Tensor
self.attention_weights: torch.Tensor
# self._init_weights()
# fmt: on
def forward(
self,
query: torch.Tensor,
key: torch.Tensor,
value: torch.Tensor,
mask: torch.BoolTensor | None = None,
) -> torch.Tensor:
"""
Notations
---------
B: Batch size
S or L: Source sequence length
T or L: Target sequence length
D: Embedding dimension
H: Number of heads
Parameters
----------
query: Although named as query, it is the embeddings `z` from the token_embedding + positional_embedding layer.
type: torch.Tensor
shape: (B, S or T, D)
key: Although named as key, it is the embeddings `z` from the token_embedding + positional_embedding layer.
type: torch.Tensor
shape: (B, S or T, D)
value: Although named as value, it is the embeddings `z` from the token_embedding + positional_embedding layer.
type: torch.Tensor
shape: (B, S or T, D)
mask: Mask to be applied to the attention scores.
type: torch.BoolTensor
shape: (B, 1, S or T, S or T)
Returns
-------
O: The output of the multi-headed attention mechanism.
type: torch.Tensor
shape: (B, S or T, D)
Variables
---------
W_Q.weight (D, D)
W_K.weight (D, D)
W_V.weight (D, D)
W_O.weight (D, D)
"""
# fmt: off
if mask is not None:
assert mask.ndim == 4, f"Mask should have 4 dimensions but got {mask.ndim}."
assert mask.shape[0] == query.shape[0], ("Batch size of mask and query must match.")
assert mask.shape[1] == 1, ("Mask should have shape (batch_size, 1, seq_len, seq_len).")
assert mask.shape[2] == mask.shape[3] == query.shape[1], ("Mask should have shape (batch_size, 1, seq_len, seq_len).")
Q = self.W_Q(query).contiguous() # Z @ W_Q -> LxD @ DxD = LxD -> [B, L, D]
K = self.W_K(key).contiguous() # Z @ W_K
V = self.W_V(value).contiguous() # Z @ W_V
Q = self.transpose_qkv(Q) # splitting happens -> [B, H, L, D]
K = self.transpose_qkv(K)
V = self.transpose_qkv(V)
# Attention
self.context_vector, self.attention_weights = self.attention(Q, K, V, mask)
context_vector_concat = self.reverse_transpose_qkv(self.context_vector)
# fmt: on
# mypy complains because it infers `O` as `Any` but it is actually a tensor.
# You can either cast it to tensor or use `self.W_O.forward(context_vector_concat)`.
O = self.W_O(context_vector_concat) # context_vector_concat @ W_O -> LxD @ DxD = LxD
return O # type: ignore[no-any-return]
def _init_weights(self) -> None:
"""See PyTorch's MultiHeadAttention code for reference."""
# we assume _qkv_same_embed_dim is True
nn.init.xavier_uniform_(self.W_Q.weight)
nn.init.xavier_uniform_(self.W_K.weight)
nn.init.xavier_uniform_(self.W_V.weight)
nn.init.xavier_uniform_(self.W_O.weight)
def transpose_qkv(self, q_or_k_or_v: torch.Tensor) -> torch.Tensor:
"""Transposition for parallel computation of multiple attention heads.
Why does transpose allow parallel computation? So originally the shape of
the query, key, and value is (B, L, D), and we want to split the D into H
heads to become (B, L, H, D / H). But this is not the shape we want (could
be due to efficiency reasons), so we transpose the shape to (B, H, L, D / H)
so all heads can be computed in parallel (efficiently).
Parameters
----------
q_or_k_or_v: The query, key, or value tensor.
type: torch.Tensor
shape: (B, L, D)
Returns
-------
q_or_k_or_v: The transposed query, key, or value tensor.
type: torch.Tensor
shape: (B, H, L, D / H)
"""
# fmt: off
# 1. q_or_k_or_v is shape (B, L, D)
# 2. aim to make it of shape (B, L, H, D / H = d_qkv)
batch_size, seq_len, _ = q_or_k_or_v.shape
q_or_k_or_v = q_or_k_or_v.view(batch_size, seq_len, self.H, self.d_model // self.H)
# 3. switch H from 3rd to 2nd dimension, or in python swap 2nd to 1st dimension and 1st to 2nd dimension
# shape (B, H, L, D / H = d_qkv)
q_or_k_or_v = q_or_k_or_v.permute(0, 2, 1, 3)
# fmt: on
return q_or_k_or_v
def reverse_transpose_qkv(self, q_or_k_or_v: torch.Tensor) -> torch.Tensor:
"""Reverse the transposition operation for concatenating multiple attention heads.
Parameters
----------
q_or_k_or_v: The query, key, or value tensor.
type: torch.Tensor
shape: (B, H, L, D / H)
Returns
-------
q_or_k_or_v: The transposed query, key, or value tensor.
type: torch.Tensor
shape: (B, L, D)
"""
# fmt: off
# 1. q_or_k_or_v is shape (B, H, L, D / H = d_qkv)
# 2. aim to make it of shape (B, L, H, D / H = d_qkv)
q_or_k_or_v = q_or_k_or_v.permute(0, 2, 1, 3)
# 3. Merge H and d_qkv into D
batch_size, seq_len, _, _ = q_or_k_or_v.shape
q_or_k_or_v = q_or_k_or_v.contiguous().view(batch_size, seq_len, self.d_model)
# fmt: on
return q_or_k_or_v
def construct_dummy_batch_future_masks(batch_size: int, seq_len: int) -> torch.BoolTensor:
"""Broadcast future mask from shape (L, L) to (B, L, L) then (B, 1, L, L)."""
# Create a lower triangular mask for a single sequence
future_mask = torch.tril(torch.ones((seq_len, seq_len), dtype=torch.bool), diagonal=0).to(torch.bool)
future_mask = future_mask.contiguous()
# broadcast future mask from shape (L, L) to (B, L, L)
future_masks = future_mask.unsqueeze(0).expand(batch_size, -1, -1)
# broadcast future mask from shape (B, L, L) to (B, 1, L, L)
future_masks = future_masks.unsqueeze(1)
return torch.BoolTensor(future_masks)
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
B, H, T, D = 1, 1, composer.block_size, composer.d_model # batch size, head, context length, embedding dimension
W_q = nn.Linear(in_features=D, out_features=D, bias=False)
W_k = nn.Linear(in_features=D, out_features=D, bias=False)
W_v = nn.Linear(in_features=D, out_features=D, bias=False)
q0 = W_q(z0_tok_embed_with_pos_embed)
k0 = W_k(z0_tok_embed_with_pos_embed)
v0 = W_v(z0_tok_embed_with_pos_embed)
pprint(q0.shape)
causal_attention = ScaledDotProductAttention()
causal_mha = MultiHeadedAttention(attention=causal_attention, H=composer.H, d_model=composer.d_model, dropout=0.0)
tril_mask = construct_dummy_batch_future_masks(B, T)
A_BHL = causal_mha(q0, k0, v0, mask=tril_mask)
attention_weights = causal_mha.attention_weights
pprint(attention_weights.shape)
show_attention_heatmaps(attention_weights, xlabel='Keys', ylabel='Queries', show_title=True)
torch.Size([1, 8, 4])
torch.Size([1, 2, 8, 8])
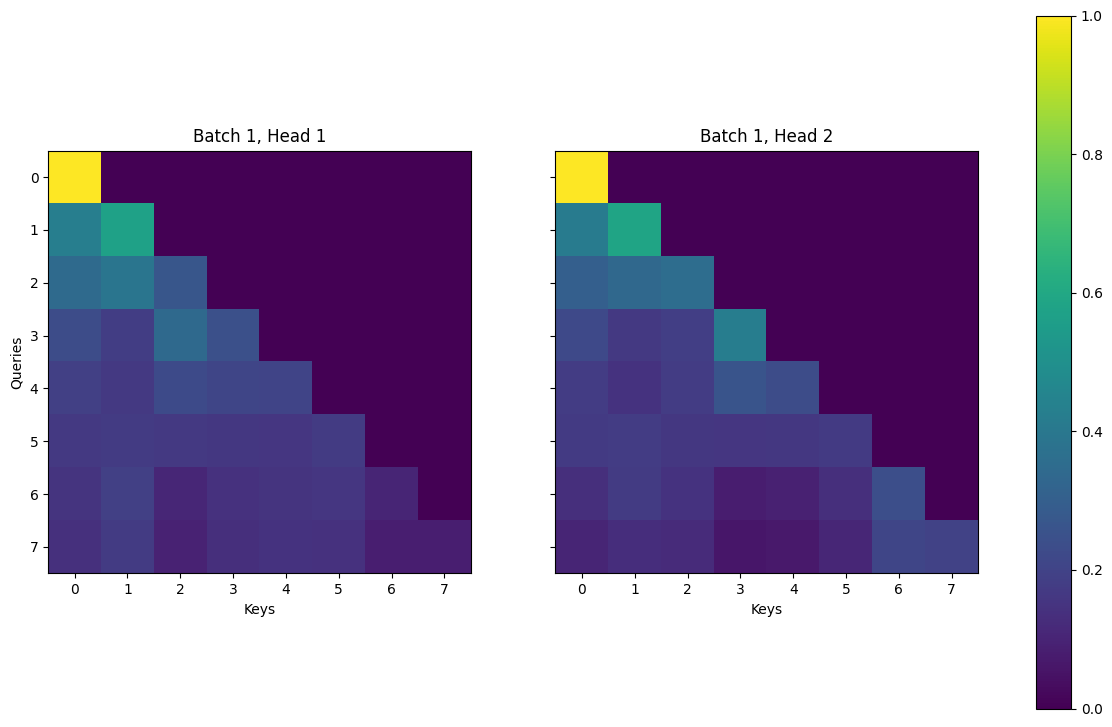
Permutation Invariance#
Neural networks without the notion of sequence will be permutation invariant with respect to the inputs and the multi-head attention mechanism is no exception. If we ignore the the batch \(\mathcal{B}\) dimension for now, then if we switch two tokens in the sequence via \(\text{permute}(\mathbf{Z})\), or more concretely, say we swap \(x_1\) and \(x_2\) in the sequence, then the output of the multi-head attention mechanism would be the same up to a permutation of the rows (\(1 <-> 2\)). This is why we would need the positional encoding to break the permutation invariance.
Some extended ideas can be found in the chapter on Numerical Stability and Initialization, from the book Dive into Deep Learning [Zhang et al., 2023].
Applying LayerNorm and Residual Connections to Multi-Head Attention Output#
Recall earlier on the discussion of using Layer Normalization (LayerNorm) on the output of the Multi-Head Attention mechanism with residual connections.
The Multi-Head Attention layer is the \(\operatorname{Sublayer}(\cdot)\) function. So \(\text{MultiHead}(\cdot) := \operatorname{Sublayer}(\cdot)\).
The output from the Multi-Head Attention to be \(\mathbf{A} \in \mathbb{R}^{T \times D}\), we would pass it to \(\operatorname{LayerNorm}(\mathbf{A} + \text{MultiHead}(\mathbf{A}))\).
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
B, H, T, D = 1, 1, composer.block_size, composer.d_model # batch size, head, context length, embedding dimension
W_q = nn.Linear(in_features=D, out_features=D, bias=False)
W_k = nn.Linear(in_features=D, out_features=D, bias=False)
W_v = nn.Linear(in_features=D, out_features=D, bias=False)
q0 = W_q(z0_tok_embed_with_pos_embed)
k0 = W_k(z0_tok_embed_with_pos_embed)
v0 = W_v(z0_tok_embed_with_pos_embed)
causal_attention = ScaledDotProductAttention()
causal_mha = MultiHeadedAttention(attention=causal_attention, H=composer.H, d_model=composer.d_model, dropout=0.0)
tril_mask = construct_dummy_batch_future_masks(B, T)
### AddNorm
add_norm_1 = AddNorm(feature_dim=composer.d_model, dropout=0.0)
z0_tok_embed_with_pos_embed_with_mha_and_addnorm1 = add_norm_1(z0_tok_embed_with_pos_embed, lambda z: causal_mha(z, z, z, mask=tril_mask))
pprint(z0_tok_embed_with_pos_embed_with_mha_and_addnorm1)
tensor([[[-1.1743, 0.7140, 1.2315, -0.7712], │ │ [-1.1786, 0.9606, 1.0212, -0.8033], │ │ [-0.4720, -0.5150, 1.7233, -0.7363], │ │ [ 0.6594, -0.4229, -1.4141, 1.1776], │ │ [-0.5698, -1.3424, 0.8061, 1.1061], │ │ [ 0.5331, 1.0998, -1.5823, -0.0506], │ │ [ 0.8590, 0.1289, 0.6803, -1.6681], │ │ [ 0.1490, -0.4571, 1.5181, -1.2100]]], grad_fn=<AddBackward0>)
Positionwise Feed-Forward Networks#
The term “positionwise feed-forward network” (FFN) in the context of Transformer models refers to a dense neural network (otherwise known as multilayer perceptron) that operates on the output of the Multi-Head Attention mechanism. This component is called “positionwise” because it applies the same feed-forward neural network (FFN) independently and identically to each position \(t\) in the sequence of length \(T\).
Independent Processing#
In the Transformer architecture, after the Multi-Head Attention mechanism aggregates information from different positions in the sequence based on attention scores, each element (or position) \(t\) in the sequence has an updated representation. The positionwise FFN then processes each of these updated representations. However, rather than considering the sequence as a whole or how elements relate to each other at this stage, the FFN operates on each position separately. This means that for a sequence of length \(T\), the same FFN is applied \(T\) times independently, and by extension, given a batch of sequences, the FFN is applied \(T \times \mathcal{B}\) times, where \(\mathcal{B}\) is the batch size.
Identical Application#
The term “using the same FFN” signifies that the same set of parameters (weights and biases) of the feed-forward neural network is used for each position in the sequence. The rationale is that the transformation is consistent across all sequence positions, so each element is transformed by the same learned function. This means the weight matrices and bias vectors of the FFN are shared across all positions in the sequence. In other words, if a sequence has \(T=3\) positions/tokens, the weight matrices and bias vectors of the FFN are the same for all three positions.
Definition#
Typically, a positionwise FFN consists of two linear transformations with a non-linear activation function in between. The general form can be represented as follows.
Definition 15 (Position-wise Feedforward Networks)
Given an input matrix \(\mathbf{Z} \in \mathbb{R}^{T \times D}\), the position-wise feedforward network computes the output matrix \(\mathbf{Z}^{\prime} \in \mathbb{R}^{T \times D}\) via the following operations:
where:
\(\mathbf{W}^{\text{FF}}_1 \in \mathbb{R}^{D \times d_{\text{ff}}}\) and \(\mathbf{W}^{\text{FF}}_2 \in \mathbb{R}^{d_{\text{ff}} \times D}\) are learnable weight matrices.
\(\mathbf{b}^{\text{FF}}_1 \in \mathbb{R}^{d_{\text{ff}}}\) and \(\mathbf{b}^{\text{FF}}_2 \in \mathbb{R}^{D}\) are learnable bias vectors.
\(\sigma_Z\) is a non-linear activation function, such as the Gaussian Error Linear Unit (GELU) or the Rectified Linear Unit (ReLU).
Projection to a Higher Dimension Space#
In the Transformer architecture, the dimensionality of the hidden layer in the positionwise FFN, denoted as \(d_{\text{ff}}\), is often chosen to be larger than the dimensionality of the input and output embeddings, \(D\). This means that the FFN projects the input embeddings into a higher-dimensional space before projecting them back to the original dimensionality.
The motivation behind this design choice is to allow the model to learn more complex and expressive representations. By projecting the input embeddings into a higher-dimensional space, the model capacity is increased, and the FFN can capture more intricate patterns and relationships among the features. We then project back (“unembedding”) the higher-dimensional representations to the original dimensionality to maintain the consistency of the model.
In practice, a common choice for the dimensionality of the hidden layer is to set \(d_{\text{ff}}\) to be a multiple of the input and output dimensionality \(D\). For example, in the original Transformer paper [Vaswani et al., 2017], the authors used \(d_{\text{ff}} = 4 \times D\).
Gaussian Error Linear Unit (GELU)#
The Gaussian Error Linear Unit (GELU) is a non-linear activation function used in the context of neural networks, which allows the model to capture more complex patterns in the data compared to traditional activation functions like ReLU. The GELU activation function is defined as:
where \(x\) is the input to the activation function, and \(\Phi(x)\) represents the cumulative distribution function (CDF) of the standard Gaussian distribution. The GELU function, effectively, models inputs with a non-linear transformation that weights inputs by their value, with a probabilistic gating mechanism derived from the Gaussian distribution.
The cumulative distribution function \(\Phi(x)\) for a standard Gaussian distribution is given by:
where \(\text{erf}\) denotes the error function, which is a special function integral of the Gaussian distribution. Combining these, the GELU function can be expressed as:
I will not pretend I have went through the entire paper and motivation of GELU, but usually, when new and “better” activation functions are proposed, they usually serve as an alternative to the common activation functions such as ReLU etc, where they solve some of the problems that the common activation functions have. From the formulation, we can see that GELU obeys the following properties:
Non-linearity: GELU introduces non-linearity to the model, a given requirement.
Differentiability: GELU is smooth and differentiable everywhere, which is beneficial for gradient-based optimization methods.
Boundedness: GELU seems to be bounded below by \(-0.17\) and not upper bounded, but practice we can show there is an upper bound if we normalize the input.
Remark 6 (Approximation of GELU)
To further simplify the GELU function and enhance computational efficiency, an approximation of the Gaussian CDF is commonly used in practice (extracted from Mathematical Analysis and Performance Evaluation of the GELU Activation Function in Deep Learning):
where \(\beta>0\) and \(\gamma \in \mathbb{R}\) are constants, selected to minimize approximation error. Substituting this approximation into the GELU function, we arrive at the final approximate form of the GELU activation function (Figure 1):
Definition 16 (GELU Activation Function)
For a matrix \(\mathbf{Z}\) with elements \(\mathbf{Z}_{t d}\) where \(t\) indexes the sequence (from 1 to \(T\) ) and \(d\) indexes the feature dimension (from 1 to \(D\) ), the GELU activation is applied element-wise to each element \(\mathbf{Z}_{t d}\) independently:
Implementation#
from typing import Optional
import torch
from torch import nn
class PositionwiseFeedForward(nn.Module):
"""
Implements a Position-wise FeedForward Network (FFN) used in Transformer models.
This module applies two linear transformations with a non-linear activation
in between. It is often used after the multi-head self-attention layer
in Transformer models.
The naming convention for the linear layers ('context_fc' and 'context_projection') is inspired by
the functionality within the Transformer architecture:
- 'context_fc' (context fully connected): This layer expands the dimensionality
of the input features, creating a richer representation. The expansion factor
is often 4 in Transformer models, meaning the intermediate size is 4 times the
size of the input/output dimensions.
- 'context_projection' (context projection): This layer projects the expanded
features back down to the original dimension, synthesizing the information
processed by the 'context_fc' layer.
"""
def __init__(
self,
d_model: int,
d_ff: Optional[int] = None,
activation: nn.Module = nn.ReLU(),
dropout: float = 0.1,
bias: bool = True,
) -> None:
super().__init__()
# fmt: off
if d_ff is None:
d_ff = 4 * d_model # typical value for d_ff in Transformer models
self.ffn = nn.ModuleDict({
'context_fc': nn.Linear(d_model, d_ff, bias=bias),
'activation': activation,
'context_projection': nn.Linear(d_ff, d_model, bias=bias),
'dropout': nn.Dropout(p=dropout, inplace=False),
})
# self._init_weights()
def _init_weights(self) -> None:
"""Initialize parameters of the linear layers."""
nn.init.xavier_uniform_(self.ffn["context_fc"].weight)
if self.ffn["context_fc"].bias is not None:
nn.init.constant_(self.ffn["context_fc"].bias, 0)
nn.init.xavier_uniform_(self.ffn["context_projection"].weight)
if self.ffn["context_projection"].bias is not None:
nn.init.constant_(self.ffn["context_projection"].bias, 0)
def forward(self, z: torch.Tensor) -> torch.Tensor:
z = self.ffn["context_fc"](z)
z = self.ffn["activation"](z)
z = self.ffn["dropout"](z)
z = self.ffn["context_projection"](z)
return z
Applying LayerNorm and Residual Connections to Positionwise FFN Output#
We also apply Layer Normalization (LayerNorm) and residual connections to the output of the positionwise FFN in a similar manner to the Multi-Head Attention.
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
ffn = PositionwiseFeedForward(d_model=composer.d_model, d_ff=composer.d_ff, activation=nn.GELU(approximate="tanh"), dropout=0.0)
### AddNorm
add_norm_2 = AddNorm(feature_dim=composer.d_model, dropout=0.0)
z0_tok_embed_with_pos_embed_with_mha_and_addnorm1_and_ffn_addnorm2 = add_norm_2(z0_tok_embed_with_pos_embed_with_mha_and_addnorm1, ffn)
pprint(z0_tok_embed_with_pos_embed_with_mha_and_addnorm1_and_ffn_addnorm2)
tensor([[[-1.1524, 1.2843, 0.6459, -0.7779], │ │ [-1.0106, 1.5607, 0.1674, -0.7176], │ │ [-0.0167, -0.9617, 1.6285, -0.6501], │ │ [ 0.8038, -0.6207, -1.3064, 1.1234], │ │ [-0.2816, -1.4653, 0.5214, 1.2255], │ │ [ 0.8419, 0.5827, -1.6964, 0.2717], │ │ [ 1.3571, -0.2673, 0.3190, -1.4089], │ │ [ 0.7333, -0.8784, 1.2301, -1.0850]]], grad_fn=<AddBackward0>)
Softmax Head#
The softmax head is the final layer of the Transformer model that maps the output of the positionwise FFN to the output vocabulary. The logits (without batch dimension) will have a shape of \(\mathbb{R}^{T \times V}\), where \(V\) is the size of the output vocabulary.
We also add another layer of Layer Normalization (LayerNorm) to the output of the positionwise FFN before the softmax head.
class Head(nn.Module):
def __init__(self, d_model: int, vocab_size: int) -> None:
super().__init__()
self.linear = nn.Linear(d_model, vocab_size)
def forward(self, z: torch.Tensor) -> torch.Tensor:
return self.linear(z)
ln_before_head = nn.LayerNorm(composer.d_model)
head = Head(d_model=composer.d_model, vocab_size=composer.vocab_size)
logits: torch.FloatTensor = head(ln_before_head(z0_tok_embed_with_pos_embed_with_mha_and_addnorm1_and_ffn_addnorm2))
pprint(logits.shape) # [B, T, V]
torch.Size([1, 8, 50257])
Each sub-sequence will be able to predict the next token in the sequence with a probability distribution over the output vocabulary \(\mathcal{V}\).
Putting it all Together to form the GPT#
Patch Composer Configuration with Model Config#
"""We use dataclass here for easy instantiating with hydra"""
from pydantic import BaseModel, Field
from torch import nn
class MultiHeadedAttentionConfig(BaseModel):
attention: Attention
d_model: int
H: int
dropout: float = 0.1
class Config:
"""Pydantic config."""
arbitrary_types_allowed = True
# TODO: add `field_validator` such that if `d_ff` is `None`, then `d_ff` is set to `4 * d_model`.
class PositionwiseFeedForwardConfig(BaseModel):
d_model: int
d_ff: int
activation: nn.Module = Field(default=nn.GELU(approximate="tanh"))
dropout: float = 0.1
bias: bool = True
class Config:
"""Pydantic config."""
arbitrary_types_allowed = True
class AddNormConfig(BaseModel):
feature_dim: int
dropout: float
class DecoderBlockConfig(BaseModel):
masked_self_attention_mha: MultiHeadedAttentionConfig
feed_forward: PositionwiseFeedForwardConfig
add_norm_1: AddNormConfig
add_norm_2: AddNormConfig
class DecoderConfig(BaseModel):
d_model: int
vocab_size: int
context_length: int # NOTE: alias=max_seq_len,block_size
num_decoder_blocks: int
dropout: float
decoder_block: DecoderBlockConfig
masked_self_attention_mha_config = MultiHeadedAttentionConfig(attention=ScaledDotProductAttention(), d_model=composer.d_model, H=composer.H, dropout=0.1)
feed_forward_config = PositionwiseFeedForwardConfig(d_model=composer.d_model, d_ff=composer.d_ff, activation=nn.GELU(approximate="tanh"), dropout=0.1, bias=True)
add_norm_config_1 = AddNormConfig(feature_dim=composer.d_model, dropout=0.1)
add_norm_config_2 = AddNormConfig(feature_dim=composer.d_model, dropout=0.1)
# Create DecoderBlockConfig
decoder_block_config = DecoderBlockConfig(
masked_self_attention_mha=masked_self_attention_mha_config,
feed_forward=feed_forward_config,
add_norm_1=add_norm_config_1,
add_norm_2=add_norm_config_2,
)
# Create the overall DecoderConfig
model_config = DecoderConfig(
d_model=composer.d_model,
vocab_size=composer.vocab_size,
context_length=composer.block_size,
num_decoder_blocks=1,
dropout=0.1,
decoder_block=decoder_block_config,
)
# patch Composer
composer.model_config = model_config
pprint(composer.model_config)
DecoderConfig( │ d_model=4, │ vocab_size=50257, │ context_length=8, │ num_decoder_blocks=1, │ dropout=0.1, │ decoder_block=DecoderBlockConfig( │ │ masked_self_attention_mha=MultiHeadedAttentionConfig( │ │ │ attention=ScaledDotProductAttention( (dropout): Dropout(p=0.0, inplace=False) ), │ │ │ d_model=4, │ │ │ H=2, │ │ │ dropout=0.1 │ │ ), │ │ feed_forward=PositionwiseFeedForwardConfig( │ │ │ d_model=4, │ │ │ d_ff=4, │ │ │ activation=GELU(approximate='tanh'), │ │ │ dropout=0.1, │ │ │ bias=True │ │ ), │ │ add_norm_1=AddNormConfig(feature_dim=4, dropout=0.1), │ │ add_norm_2=AddNormConfig(feature_dim=4, dropout=0.1) │ ) )
Decoder Blocks#
The decoder block consists of the following transformations in pseudo-code:
z = z + self.attn(self.ln_1(z))
z = z + self.mlp(self.ln_2(z))
Essentially, we take the embeddings output from the token and positional layers, and go through the following:
z -> LayerNorm(z) -> MultiHeadAttention(LayerNorm(z)) -> z + MultiHeadAttention(LayerNorm(z))
then we pass the output through the positionwise FFN, abbreivate z + MultiHeadAttention(LayerNorm(z)) as z_mha:
z_mha -> LayerNorm(z_mha) -> PositionwiseFFN(LayerNorm(z_mha)) -> z_mha + PositionwiseFFN(LayerNorm(z_mha))
It is worth noting that my implementation of AddNorm is different from the GPT-2 paper, with
self.layer_norm(x + sublayer(self.dropout(x))) instead of x + sublayer(self.layer_norm(x)).
Both works, but the former is the one mentioned in the GPT-2 paper.
class GPTDecoderBlock(nn.Module):
"""GPTDecoderBlock focuses on masked self-attention and feed-forward layers.
The architecture follows the GPT-style decoder, which only has masked
self-attention and position-wise feed-forward layers, omitting the
encoder-decoder cross-attention.
"""
def __init__(self, config: DecoderConfig) -> None:
super().__init__()
# fmt: off
self.masked_self_attention_mha = MultiHeadedAttention(**config.decoder_block.masked_self_attention_mha.model_dump(mode="python"))
self.feed_forward = PositionwiseFeedForward(**config.decoder_block.feed_forward.model_dump(mode="python"))
self.add_norm_1 = AddNorm(**config.decoder_block.add_norm_1.model_dump(mode="python"))
self.add_norm_2 = AddNorm(**config.decoder_block.add_norm_2.model_dump(mode="python"))
# fmt: on
def forward(
self,
z: torch.Tensor, # that's tgt in torch code base
*,
target_masks: torch.BoolTensor, # that's tgt_mask in torch code base
) -> torch.Tensor:
z = self.add_norm_1(
z,
lambda z: self.masked_self_attention_mha(query=z, key=z, value=z, mask=target_masks),
)
z = self.add_norm_2(z, self.feed_forward)
return z
Decoder#
from typing import cast, overload, Type
import torch
from torch import nn
from typing_extensions import override, TypeAlias
class _NotGiven:
_instance: _NotGiven | None = None
def __new__(cls: Type[_NotGiven]) -> _NotGiven: # noqa: PYI034
if cls._instance is None:
cls._instance = super(_NotGiven, cls).__new__(cls) # noqa: UP008
return cls._instance
def __bool__(self) -> Literal[False]:
"""
This method is used to define the boolean value of an instance of `_NotGiven`.
By returning `False`, it allows `_NotGiven` to be used in boolean contexts (like
`if` statements) to signify the absence of a value. This is especially useful
for checking if an argument was provided or not in a function.
"""
return False
@override
def __repr__(self) -> Literal["NOT_GIVEN"]:
return "NOT_GIVEN"
def __setattr__(self, key: str, value: Any) -> None:
raise AttributeError(f"{self.__class__.__name__} instances are immutable")
def __delattr__(self, key: str) -> None:
raise AttributeError(f"{self.__class__.__name__} instances are immutable")
NOT_GIVEN = _NotGiven()
NotGiven: TypeAlias = _NotGiven
def construct_dummy_batch_target_padding_masks(batch_size: int, seq_len: int) -> torch.BoolTensor:
"""Construct a dummy batch of target padding masks of shape (B, 1, L, L) which
assumes there is no padding token involved."""
return torch.BoolTensor(torch.ones((batch_size, 1, seq_len, seq_len), dtype=torch.bool))
class BaseDecoder(nn.Module, ABC):
"""
Abstract base class for a decoder in a transformer-like architecture.
"""
def __init__(
self,
config: DecoderConfig,
) -> None:
super().__init__()
self.config = config
@abstractmethod
def forward(
self,
input_tokens: torch.LongTensor,
*, # force keyword only arguments to prevent errors
target_padding_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
future_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
encoder_hidden_states: torch.Tensor | NotGiven = NOT_GIVEN, # that's memory in torch code base
encoder_hidden_states_masks: torch.BoolTensor | NotGiven = NOT_GIVEN, # that's memory_mask in torch code base
) -> torch.FloatTensor:
...
def _init_weights(self, module: nn.Module) -> None:
"""Initializes weights of the given module using Xavier uniform initialization."""
for p in module.parameters():
if p.dim() > 1:
nn.init.xavier_uniform_(p)
# NOTE: seq_len <= context_length == max_seq_len
class GPTDecoder(BaseDecoder):
def __init__(self, config: DecoderConfig) -> None:
super().__init__(config)
# fmt: off
self.d_model : int = config.d_model
self.tok_embed : nn.Embedding = nn.Embedding(config.vocab_size, config.d_model)
self.pos_embed : nn.Parameter = nn.Parameter(torch.zeros(1, config.context_length, config.d_model))
self.decoder_blocks: nn.ModuleList = nn.ModuleList([GPTDecoderBlock(config) for _ in range(config.num_decoder_blocks)]) # PyTorch did not make ModuleList a proper container, maybe open a PR to make it inherit Generic[T]???
self.dropout : nn.Dropout = nn.Dropout(config.dropout)
self.layer_norm : nn.LayerNorm = nn.LayerNorm(config.d_model)
self.head : nn.Linear = nn.Linear(config.d_model, config.vocab_size) # last layer
# fmt: on
self.apply(self._init_weights)
# apply special scaled init to the residual projections, per GPT-2 paper
for parameter_name, parameter in self.named_parameters():
if parameter_name.endswith("context_projection.weight"):
mean = 0.0
std_dev = 0.02 / torch.sqrt(torch.tensor(2 * config.num_decoder_blocks, dtype=torch.float))
torch.nn.init.normal_(parameter, mean=mean, std=std_dev)
@property
def total_trainable_parameters(self) -> int:
"""Returns the number of trainable parameters in the model."""
return sum(p.numel() for p in self.parameters() if p.requires_grad)
@property
def total_parameters(self) -> int:
"""Returns the total number of parameters in the model, including non-trainable."""
return sum(p.numel() for p in self.parameters())
@override
def _init_weights(self, module: nn.Module) -> None:
normal_init_modules = (nn.Linear, nn.Embedding)
if isinstance(module, normal_init_modules):
torch.nn.init.normal_(module.weight, mean=0.0, std=0.02)
if hasattr(module, "bias") and module.bias is not None:
torch.nn.init.zeros_(module.bias)
@overload
def create_target_masks(
self, batch_size: int, seq_len: int, target_padding_masks: torch.BoolTensor, future_masks: torch.BoolTensor
) -> torch.BoolTensor:
...
@overload
def create_target_masks(
self, batch_size: int, seq_len: int, target_padding_masks: torch.BoolTensor, future_masks: NotGiven
) -> torch.BoolTensor:
...
@overload
def create_target_masks(
self, batch_size: int, seq_len: int, target_padding_masks: NotGiven, future_masks: torch.BoolTensor
) -> torch.BoolTensor:
...
@overload
def create_target_masks(
self, batch_size: int, seq_len: int, target_padding_masks: NotGiven, future_masks: NotGiven
) -> torch.BoolTensor:
...
def create_target_masks(
self,
batch_size: int,
seq_len: int,
target_padding_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
future_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
) -> torch.BoolTensor:
target_masks_shape = (batch_size, 1, seq_len, seq_len)
if target_padding_masks is NOT_GIVEN and future_masks is NOT_GIVEN:
target_padding_masks = cast(
torch.BoolTensor, construct_dummy_batch_target_padding_masks(batch_size, seq_len)
)
future_masks = cast(torch.BoolTensor, construct_dummy_batch_future_masks(batch_size, seq_len))
# FIXME: CAN SOMEONE PLEASE HELP ME WITH TYPING HERE?? I AM SO STUCK IN CASTING HELL.
if target_padding_masks is NOT_GIVEN:
target_padding_masks = cast(
torch.BoolTensor, construct_dummy_batch_target_padding_masks(batch_size, seq_len)
)
if future_masks is NOT_GIVEN:
future_masks = cast(torch.BoolTensor, construct_dummy_batch_future_masks(batch_size, seq_len))
assert target_padding_masks.shape == future_masks.shape == target_masks_shape # type: ignore[union-attr]
return cast(
torch.BoolTensor,
torch.logical_and(cast(torch.Tensor, target_padding_masks), cast(torch.Tensor, future_masks)).bool(),
)
def forward(
self,
input_tokens: torch.LongTensor,
*, # force keyword only arguments to prevent errors
target_padding_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
future_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
# fmt: off
encoder_hidden_states: torch.Tensor | NotGiven = NOT_GIVEN, # that's memory in torch code base and is ensured not used here
encoder_hidden_states_masks: torch.BoolTensor | NotGiven = NOT_GIVEN,
# that's memory_mask in torch code base and is ensured not used here
# fmt: on
) -> torch.FloatTensor:
assert encoder_hidden_states is NOT_GIVEN, "GPTDecoderBlock does not have encoder-decoder cross-attention"
assert encoder_hidden_states_masks is NOT_GIVEN, "GPTDecoderBlock does not have encoder-decoder cross-attention"
# fmt: off
batch_size : int = input_tokens.size(0)
seq_len : int = input_tokens.size(1) # note seq_len <= context_length in decoder
target_masks: torch.BoolTensor = self.create_target_masks(batch_size=batch_size, seq_len=seq_len, target_padding_masks=target_padding_masks, future_masks=future_masks)
target_masks = target_masks.to(input_tokens.device) # type: ignore[assignment]
z = self.tok_embed(input_tokens) # * math.sqrt(self.d_model) for better optimization landscape
z = z + self.pos_embed[:, :seq_len, :]
z = self.dropout(z)
for decoder_block in self.decoder_blocks:
z = decoder_block(z, target_masks=target_masks)
z = self.layer_norm(z)
logits: torch.FloatTensor = self.head(z)
# fmt: on
return logits
@torch.no_grad()
def generate(
self,
starting_tokens: torch.LongTensor | List[int], # alias is starting_tokens
*,
max_tokens: int = 100, # max tokens to generate
temperature: float = 1.0, # temperature for sampling
greedy: bool = False, # if True, sample greedily
top_k: int | None = None, # if not None, sample from top k tokens
top_p: float | None = None, # neclueus sampling
) -> torch.LongTensor:
if self.training:
# a safety check to make sure we are not in training mode
# this generate could be called outside after training, or during
# training as a form of validation/evaluation.
self.eval()
# NOTE: `starting_tokens` is a list of integers, or a torch.LongTensor of shape (S or T).
# the distinction between this `starting_tokens` versus the one in `forward` is this is
# not batched! It is a single sequence of tokens so in order for it to be compatible
# with the model, we need to expand the first dimension to 1 - making it a batch.
if isinstance(starting_tokens, list):
starting_tokens = cast(torch.LongTensor, torch.as_tensor(starting_tokens, dtype=torch.long)[None, ...])
if starting_tokens.dim() == 1:
starting_tokens = cast(torch.LongTensor, torch.as_tensor(starting_tokens, dtype=torch.long)[None, ...]) # type: ignore[no-redef]
assert starting_tokens.dim() == 2, "starting_tokens must be a 1D or 2D tensor"
for _ in range(max_tokens):
# if the sequence context is growing too long we must crop it at context_length
starting_tokens_cropped = (
starting_tokens[:, -self.config.context_length :]
if starting_tokens.size(1) > self.config.context_length
else starting_tokens
)
batch_size = starting_tokens_cropped.size(0)
seq_len = starting_tokens_cropped.size(1) # this must be less than or equal to self.config.context_length
target_padding_masks = construct_dummy_batch_target_padding_masks(batch_size, seq_len)
future_masks = construct_dummy_batch_future_masks(batch_size, seq_len)
logits = self(
starting_tokens_cropped,
target_padding_masks=target_padding_masks,
future_masks=future_masks,
)
assert logits.shape == (batch_size, seq_len, self.config.vocab_size)
# NOTE: we are only interested in the last token's logits because in
# autoregressive models, the last token's logits holds the contextual
# information of all previous tokens (because it is the only token
# not masked). But in any case, we need this last token's logits to
# sample the next token.
logits = logits[:, -1, :] # shape: (batch_size, vocab_size)
assert logits.shape == (batch_size, self.config.vocab_size)
# now scale by temperature
logits = logits / (temperature + 1e-8) # add epsilon to prevent division by zero
# optional cropping of logits to top k
if top_k is not None:
top_k_values, _ = torch.topk(logits, k=top_k)
# The masking out to -inf is to prevent the sampling from
# non-top k values, effectively making the sampling pool
# to be only the top k values. We are zeroing out the
# probabilities of non-top k values.
logits[logits < top_k_values[:, [-1]]] = float("-inf")
if top_p is not None:
def top_p_logits(logits: torch.Tensor, p: float) -> torch.Tensor:
sorted_logits, sorted_indices = torch.sort(logits, descending=True)
cumulative_probs = torch.cumsum(torch.softmax(sorted_logits, dim=-1), dim=-1)
# Remove tokens with cumulative probability above the threshold
sorted_indices_to_remove = cumulative_probs > p
# Shift the indices to the right to keep also the first token above the threshold
sorted_indices_to_remove[..., 1:] = sorted_indices_to_remove[..., :-1].clone()
sorted_indices_to_remove[..., 0] = 0
# Scatter sorted tensors to original indexing
indices_to_remove = sorted_indices.scatter(
dim=-1, index=sorted_indices, src=sorted_indices_to_remove
)
logits[indices_to_remove] = float("-inf")
return logits
logits = top_p_logits(logits, top_p)
probs = torch.softmax(logits, dim=-1)
next_token = (
torch.multinomial(probs, num_samples=1) if not greedy else torch.topk(probs, k=1, dim=-1).indices
)
# append the next token to the input tokens, aka append sampled index
# to the running sequence context and continue the generation
starting_tokens = torch.cat([starting_tokens, next_token], dim=1) # type: ignore[assignment]
return starting_tokens
generator = torch.Generator(device=composer.device)
generator.manual_seed(25)
seed_all(composer.seed, seed_torch=True, set_torch_deterministic=False)
train_batch = get_batch(composer, split="train", batch_size=composer.batch_size, block_size=composer.block_size, device=composer.device, generator=generator)
x, y = train_batch
assert x.shape == (composer.batch_size, composer.block_size)
model = GPTDecoder(model_config).to(composer.device)
pprint(model.total_trainable_parameters)
logits = model(x)
assert logits.shape == (composer.batch_size, composer.block_size, composer.vocab_size)
452473
To this end, we have covered the implementations of the GPT-2 architecture, for the training and inference mechanism, please see the next series.
References and Further Readings#
References
Residual Connection and Layer Normalization - Dive into Deep Learning
Self-Attention and Positional Encoding - Dive into Deep Learning
The Illustrated GPT-2 (Visualizing Transformer Language Models) - Jay Alammar
Some Intuition on Attention and the Transformer - Eugene Yan
Let’s build GPT: from scratch, in code, spelled out - Andrej Karpathy
Why does the transformer do better than RNN and LSTM in long-range context dependencies?
Neural Machine Translation by Jointly Learning to Align and Translate - arXiv
Numerical Stability and Initialization - Dive into Deep Learning
Why can we approximate the joint probability distribution using the output vector of the GPT model?
Why Joint Probability in Generative Models? - Data Science Stack Exchange
CSC412 Winter 2020: Probabilsitic Machine Learning - University of Toronto
GPT-1, GPT-2, GPT-3, InstructGPT, ChatGPT, and GPT-4 Summary






