Easy - Hot Potatoes

Easy - Hot Potatoes#

Problem#

Question details can be found here.

Constraints and Assumptions#

Placeholder.

Implementation#

  • num = 5 means when the counter reaches 5, the person holding the potato will be eliminated.

  • d, c, b, a (a is the first in queue and he holds the potato, counter starts at 0)

  • a, d, c, b (b holds the potato, counter is 1)

  • b, a, d, c (c holds the potato, counter is 2)

  • c, b, a, d (d holds the potato, counter is 3)

  • d, c, b, a (a holds the potato, counter is 4)

  • a, d, c, b (b holds the potato, counter is 5, b is eliminated)

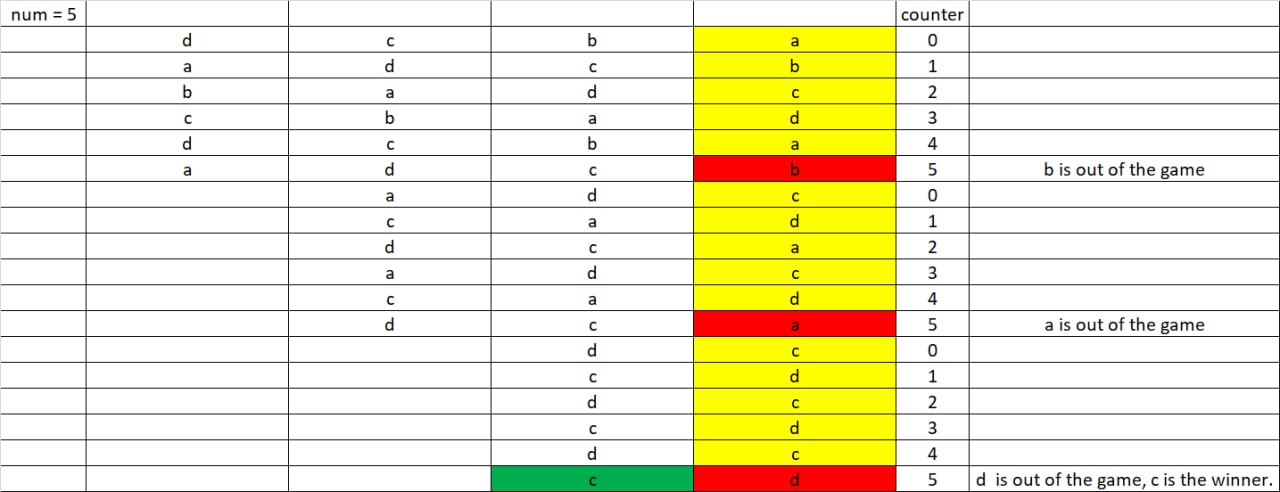
../../../_images/hot_potato.jpg

Fig. 61 Hot Potato elimination diagram, with 4 people and num set to 5.#

@dataclass(frozen=False, init=True)
class Solution:
    counter: int = 0
    q: QueueList[str] = field(default_factory=QueueList)

    def hot_potato(self, names: List[str], num: int) -> str:
        for name in names:
            self.q.enqueue(name)

        while self.q.size > 1:
            first_in_q = self.q.dequeue()
            self.q.enqueue(first_in_q)

            self.counter += 1
            if self.counter == num:
                self.q.dequeue()
                self.counter = 0  # reset

        return self.q.dequeue()

Note ["Bill", "David", "Susan", "Jane"] means Bill is first in queue.

print(Solution().hot_potato(names=["Bill", "David", "Susan", "Jane"], num=5)) # Susan

Susan

Time Complexity#

Assume the input names to be a list of length \(n\).

From Time Complexity of Queue Implemented using List, dequeue is of \(\O(1)\) since it uses pop while enqueue is \(\O(n)\) since it uses insert.

And since we traverse the given list once to enqueue first, we would already have \(n\) times of enqueue which is \(\O(n) \times n \approx \O(n^2)\)[1].

Subsequently, we enter a while loop, which at worst can take \(n\) iterations, which eventually leads to \(\O(n^2) + \O(n^2) + \O(n) \approx \O(n^2)\).

Space Complexity#

Assume the queue q has length \(n\).

The space complexity is at most \(\O(n)\) as we are just maintaining a queue with at most \(n\) elements inside.