Implementation#
This section implements the linear regression algorithm from scratch.
r"""Linear Regression Class.
High-level module implementing linear regression with support for multiple
solvers and regularization.
Features:
- Closed Form Solution
- Batch Gradient Descent
- Stochastic Gradient Descent
Supports L1 and L2 regularization.
NOTE:
1. Regularization parameter `C` is only applicable when `regularization` is set.
2. Ensure that input data does not contain NaN or infinite values.
"""
from __future__ import annotations
import functools
import logging
from typing import Any, Callable, List, Optional, TypeVar
import numpy as np
from numpy.typing import NDArray
from sklearn.exceptions import NotFittedError
from typing_extensions import Concatenate, ParamSpec
logging.basicConfig(level=logging.INFO, format="%(asctime)s - %(levelname)s - %(message)s")
P = ParamSpec("P")
T = TypeVar("T")
def not_fitted(func: Callable[Concatenate[LinearRegression, P], T]) -> Callable[Concatenate[LinearRegression, P], T]:
@functools.wraps(func)
def wrapper(self: LinearRegression, *args: P.args, **kwargs: P.kwargs) -> T:
if not self._fitted:
raise NotFittedError
else:
return func(self, *args, **kwargs)
return wrapper
class MyLinearRegression:
"""
Linear Regression model supporting multiple solvers and regularization.
Attributes
----------
coef_ : NDArray[np.floating[Any]]
Coefficient vector.
intercept_ : float
Intercept term.
has_intercept : bool
Whether to include an intercept in the model.
solver : str
Solver type: {"Closed Form Solution", "Batch Gradient Descent",
"Stochastic Gradient Descent"}.
learning_rate : float
Learning rate for gradient descent solvers.
loss_function : LossFunction
Loss function to be minimized.
regularization : Optional[str]
Type of regularization: {"l1", "l2"} or None.
C : Optional[float]
Regularization strength. Must be a positive float.
num_epochs : int
Number of epochs for gradient descent solvers.
_fitted : bool
Flag indicating whether the model has been fitted.
loss_history : List[float]
History of loss values during training.
optimal_betas : NDArray[np.floating[Any]]
Optimal beta coefficients after fitting.
"""
def __init__(
self,
has_intercept: bool = True,
solver: str = "Closed Form Solution",
learning_rate: float = 0.1,
loss_function: Optional[Any] = None,
regularization: Optional[str] = None,
C: Optional[float] = None,
num_epochs: Optional[int] = 1000,
) -> None:
"""
Initialize the Linear Regression model with specified parameters.
Parameters
----------
has_intercept : bool, default=True
Whether to include an intercept in the model.
solver : str, default="Closed Form Solution"
Solver type: {"Closed Form Solution", "Batch Gradient Descent", "Stochastic Gradient Descent"}.
learning_rate : float, default=0.01
Learning rate for gradient descent solvers.
loss_function : LossFunction, default=LossFunction.l2_loss()
Loss function to be minimized.
regularization : Optional[str], default=None
Type of regularization: {"l1", "l2"} or None.
C : Optional[float], default=None
Regularization strength. Must be a positive float.
num_epochs : int, default=1000
Number of epochs for gradient descent solvers.
"""
self.solver = solver
self.has_intercept = has_intercept
self.learning_rate = learning_rate
self.loss_function = loss_function or self.l2_loss
self.regularization = regularization
self.C = C
self.num_epochs = num_epochs
self.coef_: NDArray[np.floating[Any]]
self.intercept_: float | None = None
self._fitted: bool = False
self.optimal_betas: NDArray[np.floating[Any]]
self.loss_history: List[float] = []
# Validate regularization parameters
if self.regularization is not None and self.C is None:
raise ValueError("Regularization strength 'C' must be provided when using regularization.")
if self.regularization not in {None, "l1", "l2"}:
raise ValueError("Regularization must be one of {None, 'l1', 'l2'}.")
# Validate solver
valid_solvers = {"Closed Form Solution", "Batch Gradient Descent", "Stochastic Gradient Descent"}
if self.solver not in valid_solvers:
raise ValueError(f"Solver must be one of {valid_solvers}.")
@staticmethod
def l2_loss(y_true: NDArray[np.floating[Any]], y_pred: NDArray[np.floating[Any]]) -> float:
return np.square(y_true - y_pred).mean() # type: ignore[no-any-return]
def _add_regularization(self, loss: float, w: NDArray[np.floating[Any]]) -> float:
"""
Apply regularization to the loss.
Parameters
----------
loss : float
Current loss value.
w : NDArray[np.floating[Any]]
Weight vector.
Returns
-------
float
Updated loss with regularization.
"""
if self.regularization == "l1":
loss += self.C * np.abs(w[1:]).sum()
elif self.regularization == "l2":
assert self.C is not None
loss += (0.5 * self.C) * np.square(w[1:]).sum()
return loss
def _initialize_weights(self, n_features: int) -> NDArray[np.floating[Any]]:
"""
Initialize weights for gradient descent solvers.
Parameters
----------
n_features : int
Number of features.
Returns
-------
NDArray[np.floating[Any]]
Initialized weight vector.
"""
return np.zeros((n_features, 1))
def _check_input_shapes(
self, X: NDArray[np.floating[Any]], y_true: NDArray[np.floating[Any]]
) -> tuple[NDArray[np.floating[Any]], NDArray[np.floating[Any]]]:
"""
Validate and reshape input data.
Parameters
----------
X : NDArray[np.floating[Any]]
Input feature matrix.
y_true : NDArray[np.floating[Any]]
True target values.
Returns
-------
tuple[NDArray[np.floating[Any]], NDArray[np.floating[Any]]]
Reshaped feature matrix and target vector.
"""
if X.ndim == 1:
X = X.reshape(-1, 1)
logging.info("Reshaped X to 2D array with shape %s.", X.shape)
if y_true.ndim == 1:
y_true = y_true.reshape(-1, 1)
logging.info("Reshaped y_true to 2D array with shape %s.", y_true.shape)
if X.shape[0] != y_true.shape[0]:
raise ValueError("Number of samples in X and y_true must be equal.")
return X, y_true
def fit(self, X: NDArray[np.floating[Any]], y_true: NDArray[np.floating[Any]]) -> LinearRegression:
"""
Fit the Linear Regression model to the data.
Parameters
----------
X : NDArray[np.floating[Any]]
Input feature matrix of shape (n_samples, n_features).
y_true : NDArray[np.floating[Any]]
True target values of shape (n_samples,).
Returns
-------
LinearRegression
The fitted model.
"""
X, y_true = self._check_input_shapes(X, y_true)
# Add intercept term if necessary
if self.has_intercept:
X = np.insert(X, 0, 1, axis=1)
logging.info("Added intercept term to X.")
n_samples, n_features = X.shape
logging.info("Fitting model with %d samples and %d features.", n_samples, n_features)
if self.solver == "Closed Form Solution":
XtX = X.T @ X
det = np.linalg.det(XtX)
if det == 0:
logging.warning("Singular matrix encountered. Using pseudo-inverse instead.")
XtX_inv = np.linalg.pinv(XtX)
else:
XtX_inv = np.linalg.inv(XtX)
Xty = X.T @ y_true
self.optimal_betas = XtX_inv @ Xty
logging.info("Computed optimal betas using Closed Form Solution.")
elif self.solver in {"Batch Gradient Descent", "Stochastic Gradient Descent"}:
assert self.num_epochs is not None
self.optimal_betas = self._initialize_weights(n_features)
logging.info("Initialized weights for Gradient Descent.")
for epoch in range(1, self.num_epochs + 1):
if self.solver == "Batch Gradient Descent":
y_pred = X @ self.optimal_betas
elif self.solver == "Stochastic Gradient Descent":
indices = np.random.permutation(n_samples) # noqa: NPY002
for i in indices:
xi = X[i].reshape(1, -1)
yi = y_true[i]
y_pred = xi @ self.optimal_betas
error = y_pred - yi
gradient = xi.T @ error
if self.regularization == "l2":
assert self.C is not None
gradient[1:] += self.C * self.optimal_betas[1:]
elif self.regularization == "l1":
gradient[1:] += self.C * np.sign(self.optimal_betas[1:])
self.optimal_betas -= self.learning_rate * gradient
continue # Skip the rest of the loop for SGD
error = y_pred - y_true
loss = self.loss_function(y_true=y_true, y_pred=y_pred)
loss = self._add_regularization(loss, self.optimal_betas)
self.loss_history.append(loss)
gradient = (2 / n_samples) * (X.T @ error)
if self.regularization == "l2":
assert self.C is not None
gradient[1:] += self.C * self.optimal_betas[1:]
elif self.regularization == "l1":
gradient[1:] += self.C * np.sign(self.optimal_betas[1:])
self.optimal_betas -= self.learning_rate * gradient
if epoch % 100 == 0 or epoch == 1:
logging.info("Epoch %d | Loss: %.4f", epoch, loss)
# Set coefficients and intercept
if self.has_intercept:
self.intercept_ = float(self.optimal_betas[0])
self.coef_ = self.optimal_betas[1:].flatten()
logging.info("Set intercept and coefficients.")
else:
self.coef_ = self.optimal_betas.flatten()
self.intercept_ = 0.0
logging.info("Set coefficients without intercept.")
self._fitted = True
logging.info("Model fitting complete.")
return self
@not_fitted
def predict(self, X: NDArray[np.floating[Any]]) -> NDArray[np.floating[Any]]:
"""
Predict target values using the fitted model.
Parameters
----------
X : NDArray[np.floating[Any]]
Input feature matrix of shape (n_samples, n_features).
Returns
-------
NDArray[np.floating[Any]]
Predicted target values of shape (n_samples,).
"""
if self.has_intercept:
X = np.insert(X, 0, 1, axis=1)
assert self.optimal_betas is not None
y_pred = X @ self.optimal_betas
return y_pred.flatten()
def residuals(self, X: NDArray[np.floating[Any]], y_true: NDArray[np.floating[Any]]) -> NDArray[np.floating[Any]]:
"""
Calculate residuals between true and predicted values.
Parameters
----------
X : NDArray[np.floating[Any]]
Input feature matrix.
y_true : NDArray[np.floating[Any]]
True target values.
Returns
-------
NDArray[np.floating[Any]]
Residuals of shape (n_samples,).
"""
y_pred = self.predict(X)
residuals = y_true.flatten() - y_pred
return residuals
@not_fitted
def score(self, X: NDArray[np.floating[Any]], y_true: NDArray[np.floating[Any]]) -> float:
"""
Calculate the coefficient of determination R^2 of the prediction.
Parameters
----------
X : NDArray[np.floating[Any]]
Input feature matrix.
y_true : NDArray[np.floating[Any]]
True target values.
Returns
-------
float
R^2 score.
"""
y_pred = self.predict(X)
ss_total = np.sum((y_true.flatten() - np.mean(y_true)) ** 2)
ss_res = np.sum((y_true.flatten() - y_pred) ** 2)
r2_score = 1 - (ss_res / ss_total)
return float(r2_score)
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
from rich.pretty import pprint
def regression_test(solver: str = "Closed Form Solution") -> None:
np.random.seed(1930)
X, y_true = make_regression(
n_samples=10000, n_features=10, random_state=1930, coef=False
) # returns 2-d array of 1000 by 10
x_train, x_val, y_train, y_val = train_test_split(X, y_true, test_size=0.3, random_state=1930)
lr_SKLEARN = LinearRegression(fit_intercept=True).fit(x_train, y_train)
lr_CUSTOM = MyLinearRegression(solver=solver, has_intercept=True, num_epochs=10000).fit(x_train, y_train)
# Debugged, the intercept is the one with major difference why? Answer: https://stackoverflow.com/questions/66881829/implementation-of-linear-regression-closed-form-solution/66886954?noredirect=1#comment118259946_66886954
pprint(lr_CUSTOM.intercept_)
pprint(lr_SKLEARN.intercept_)
pprint(lr_CUSTOM.coef_)
pprint(lr_SKLEARN.coef_)
pred_CUSTOM = lr_CUSTOM.predict(x_val)
pred_SKLEARN = lr_SKLEARN.predict(x_val)
print("First Value HN", pred_CUSTOM[0])
print("First Value SKLEARN", pred_SKLEARN[0])
print("HN MSE", mean_squared_error(y_val, pred_CUSTOM))
print("SKLEARN MSE", mean_squared_error(y_val, pred_SKLEARN))
regression_test()
2024-12-17 09:44:40,332 - INFO - Reshaped y_true to 2D array with shape (7000, 1).
2024-12-17 09:44:40,333 - INFO - Added intercept term to X.
2024-12-17 09:44:40,334 - INFO - Fitting model with 7000 samples and 11 features.
2024-12-17 09:44:40,339 - INFO - Computed optimal betas using Closed Form Solution.
/tmp/ipykernel_2821/987029641.py:292: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
self.intercept_ = float(self.optimal_betas[0])
2024-12-17 09:44:40,340 - INFO - Set intercept and coefficients.
2024-12-17 09:44:40,341 - INFO - Model fitting complete.
-2.9976021664879227e-15
4.163336342344337e-15
array([65.74652523, 19.51408752, 32.05245375, 50.32013901, 52.76364276, │ │ 4.69437951, 47.88858774, 69.03001556, 30.41026743, 3.47178546])
array([65.74652523, 19.51408752, 32.05245375, 50.32013901, 52.76364276, │ │ 4.69437951, 47.88858774, 69.03001556, 30.41026743, 3.47178546])
First Value HN 183.222001509455
First Value SKLEARN 183.22200150945545
HN MSE 9.907315629326824e-27
SKLEARN MSE 2.2502265868963244e-25
def regression_diabetes() -> None:
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
lr_SKLEARN = LinearRegression()
lr_CUSTOM = MyLinearRegression(has_intercept=True, solver="Batch Gradient Descent", num_epochs=6666)
lr_CUSTOM.fit(diabetes_X_train, diabetes_y_train)
lr_SKLEARN.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = lr_SKLEARN.predict(diabetes_X_test)
pred_CUSTOM = lr_CUSTOM.predict(diabetes_X_test)
# The coefficients
print("SKLEARN Coefficients:", lr_SKLEARN.coef_)
print("HONGNAN Coefficients:", lr_CUSTOM.coef_)
# The mean squared error
print("HN MSE", mean_squared_error(diabetes_y_test, pred_CUSTOM))
print("SKLEARN MSE", mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print("Coefficient of determination: %.2f" % r2_score(diabetes_y_test, diabetes_y_pred))
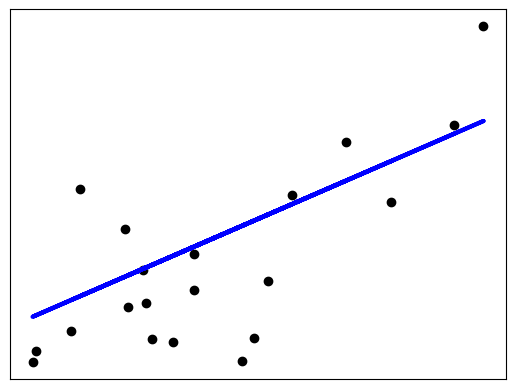
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color="black")
plt.plot(diabetes_X_test, diabetes_y_pred, color="blue", linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
regression_diabetes()
2024-12-17 09:44:40,422 - INFO - Reshaped y_true to 2D array with shape (422, 1).
2024-12-17 09:44:40,423 - INFO - Added intercept term to X.
2024-12-17 09:44:40,424 - INFO - Fitting model with 422 samples and 2 features.
2024-12-17 09:44:40,426 - INFO - Initialized weights for Gradient Descent.
2024-12-17 09:44:40,427 - INFO - Epoch 1 | Loss: 29468.6469
2024-12-17 09:44:40,431 - INFO - Epoch 100 | Loss: 5777.2529
2024-12-17 09:44:40,434 - INFO - Epoch 200 | Loss: 5619.4054
2024-12-17 09:44:40,438 - INFO - Epoch 300 | Loss: 5475.2313
2024-12-17 09:44:40,442 - INFO - Epoch 400 | Loss: 5343.5459
2024-12-17 09:44:40,446 - INFO - Epoch 500 | Loss: 5223.2675
2024-12-17 09:44:40,450 - INFO - Epoch 600 | Loss: 5113.4080
2024-12-17 09:44:40,453 - INFO - Epoch 700 | Loss: 5013.0648
2024-12-17 09:44:40,457 - INFO - Epoch 800 | Loss: 4921.4137
2024-12-17 09:44:40,461 - INFO - Epoch 900 | Loss: 4837.7017
2024-12-17 09:44:40,465 - INFO - Epoch 1000 | Loss: 4761.2411
2024-12-17 09:44:40,469 - INFO - Epoch 1100 | Loss: 4691.4037
2024-12-17 09:44:40,472 - INFO - Epoch 1200 | Loss: 4627.6159
2024-12-17 09:44:40,476 - INFO - Epoch 1300 | Loss: 4569.3536
2024-12-17 09:44:40,480 - INFO - Epoch 1400 | Loss: 4516.1381
2024-12-17 09:44:40,484 - INFO - Epoch 1500 | Loss: 4467.5323
2024-12-17 09:44:40,487 - INFO - Epoch 1600 | Loss: 4423.1369
2024-12-17 09:44:40,491 - INFO - Epoch 1700 | Loss: 4382.5872
2024-12-17 09:44:40,495 - INFO - Epoch 1800 | Loss: 4345.5500
2024-12-17 09:44:40,499 - INFO - Epoch 1900 | Loss: 4311.7210
2024-12-17 09:44:40,502 - INFO - Epoch 2000 | Loss: 4280.8225
2024-12-17 09:44:40,506 - INFO - Epoch 2100 | Loss: 4252.6005
2024-12-17 09:44:40,510 - INFO - Epoch 2200 | Loss: 4226.8231
2024-12-17 09:44:40,513 - INFO - Epoch 2300 | Loss: 4203.2787
2024-12-17 09:44:40,515 - INFO - Epoch 2400 | Loss: 4181.7737
2024-12-17 09:44:40,518 - INFO - Epoch 2500 | Loss: 4162.1316
2024-12-17 09:44:40,520 - INFO - Epoch 2600 | Loss: 4144.1910
2024-12-17 09:44:40,523 - INFO - Epoch 2700 | Loss: 4127.8044
2024-12-17 09:44:40,526 - INFO - Epoch 2800 | Loss: 4112.8373
2024-12-17 09:44:40,528 - INFO - Epoch 2900 | Loss: 4099.1666
2024-12-17 09:44:40,531 - INFO - Epoch 3000 | Loss: 4086.6802
2024-12-17 09:44:40,533 - INFO - Epoch 3100 | Loss: 4075.2754
2024-12-17 09:44:40,535 - INFO - Epoch 3200 | Loss: 4064.8585
2024-12-17 09:44:40,537 - INFO - Epoch 3300 | Loss: 4055.3439
2024-12-17 09:44:40,539 - INFO - Epoch 3400 | Loss: 4046.6535
2024-12-17 09:44:40,541 - INFO - Epoch 3500 | Loss: 4038.7159
2024-12-17 09:44:40,543 - INFO - Epoch 3600 | Loss: 4031.4659
2024-12-17 09:44:40,546 - INFO - Epoch 3700 | Loss: 4024.8439
2024-12-17 09:44:40,548 - INFO - Epoch 3800 | Loss: 4018.7956
2024-12-17 09:44:40,550 - INFO - Epoch 3900 | Loss: 4013.2711
2024-12-17 09:44:40,553 - INFO - Epoch 4000 | Loss: 4008.2252
2024-12-17 09:44:40,555 - INFO - Epoch 4100 | Loss: 4003.6164
2024-12-17 09:44:40,557 - INFO - Epoch 4200 | Loss: 3999.4068
2024-12-17 09:44:40,559 - INFO - Epoch 4300 | Loss: 3995.5619
2024-12-17 09:44:40,562 - INFO - Epoch 4400 | Loss: 3992.0500
2024-12-17 09:44:40,564 - INFO - Epoch 4500 | Loss: 3988.8423
2024-12-17 09:44:40,566 - INFO - Epoch 4600 | Loss: 3985.9125
2024-12-17 09:44:40,568 - INFO - Epoch 4700 | Loss: 3983.2365
2024-12-17 09:44:40,571 - INFO - Epoch 4800 | Loss: 3980.7923
2024-12-17 09:44:40,573 - INFO - Epoch 4900 | Loss: 3978.5598
2024-12-17 09:44:40,575 - INFO - Epoch 5000 | Loss: 3976.5207
2024-12-17 09:44:40,578 - INFO - Epoch 5100 | Loss: 3974.6582
2024-12-17 09:44:40,579 - INFO - Epoch 5200 | Loss: 3972.9571
2024-12-17 09:44:40,582 - INFO - Epoch 5300 | Loss: 3971.4033
2024-12-17 09:44:40,584 - INFO - Epoch 5400 | Loss: 3969.9841
2024-12-17 09:44:40,586 - INFO - Epoch 5500 | Loss: 3968.6879
2024-12-17 09:44:40,589 - INFO - Epoch 5600 | Loss: 3967.5039
2024-12-17 09:44:40,590 - INFO - Epoch 5700 | Loss: 3966.4225
2024-12-17 09:44:40,592 - INFO - Epoch 5800 | Loss: 3965.4348
2024-12-17 09:44:40,594 - INFO - Epoch 5900 | Loss: 3964.5326
2024-12-17 09:44:40,600 - INFO - Epoch 6000 | Loss: 3963.7086
2024-12-17 09:44:40,602 - INFO - Epoch 6100 | Loss: 3962.9559
2024-12-17 09:44:40,604 - INFO - Epoch 6200 | Loss: 3962.2685
2024-12-17 09:44:40,606 - INFO - Epoch 6300 | Loss: 3961.6406
2024-12-17 09:44:40,608 - INFO - Epoch 6400 | Loss: 3961.0671
2024-12-17 09:44:40,610 - INFO - Epoch 6500 | Loss: 3960.5432
2024-12-17 09:44:40,612 - INFO - Epoch 6600 | Loss: 3960.0648
/tmp/ipykernel_2821/987029641.py:292: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
self.intercept_ = float(self.optimal_betas[0])
2024-12-17 09:44:40,613 - INFO - Set intercept and coefficients.
2024-12-17 09:44:40,614 - INFO - Model fitting complete.
SKLEARN Coefficients: [938.23786125]
HONGNAN Coefficients: [892.45056539]
HN MSE 2604.751428467252
SKLEARN MSE 2548.07239872597
Coefficient of determination: 0.47
