Implement Queue using Stacks

Implement Queue using Stacks#

Twitter Handle LinkedIn Profile GitHub Profile LeetCode Problem Difficulty

Problem#

Implement a First-In-First-Out (FIFO) queue using only two stacks. The implemented queue should support all the functions of a normal queue, which are: push, peek, pop, and empty.

The class MyQueue should include the following methods:

  • push(int x): Pushes element x to the back of the queue.

  • pop(): Removes the element from the front of the queue and returns it.

  • peek(): Returns the element at the front of the queue.

  • empty(): Returns True if the queue is empty, False otherwise.

Intuition#

Our main challenge here is that stacks are Last-In-First-Out (LIFO) structures, but we need to implement a First-In-First-Out (FIFO) structure using them. We can solve this problem by using two stacks, where one stack serves as a reversing mechanism.

When we push elements into the queue, we push them into the first stack. To pop an element, we need to get it from the bottom of the first stack. However, because we can only remove elements from the top in a stack, we transfer all elements from the first stack to the second stack, which reverses the order of the elements. Then, we can simply pop the top element from the second stack.

One easy way out which also works is just use one stack and use insert to push elements to the bottom of the stack. However, this is not a good solution because insert is an expensive operation. It takes \(O(n)\) time to insert an element to the bottom of a stack of size \(n\).

Assumptions#

  • You must only utilize the standard operations of a stack: pushing to the top, peeking/popping from the top, checking its size, and checking if it’s empty.

  • Depending on your programming language, stacks might not be supported natively. However, you can simulate a stack using a list or a deque (double-ended queue) as long as you stick to the stack’s standard operations.

  • In our examples, we’ll be using Python’s list to represent a stack. We will be using two stacks:

    • The enqueue stack: This stack is used for the push operation. In this stack, an element that is pushed first will be on the bottom and the element pushed last will be on the top. For instance, if we push 1, 2, 3, and 4 in this order, our enqueue stack will look like [1, 2, 3, 4]. Here, 1 is at the front of the queue (the bottom of the stack) and 4 is at the back of the queue (the top of the stack).

    • The dequeue stack: This stack is used for the pop and peek operations. The order of the elements in this stack is the reverse of their order in the enqueue stack. If our enqueue stack is [1, 2, 3, 4], our dequeue stack will be [4, 3, 2, 1]. In this case, 1 is still at the front of the queue (now the top of the stack) and 4 is at the back of the queue (now the bottom of the stack).

Constraints#

  • The value that can be pushed into the queue (x) is constrained by the range:

    \[ 1 \leq x \leq 9. \]

  • The total number of function calls made to push, pop, peek, and empty will not exceed 100.

  • All calls to pop and peek functions will be valid.

What are Constraints for?#

In programming problems, constraints are set to define the scope and limits of the problem. They help us determine the feasible approaches and solutions for the problem by providing information about the range and characteristics of the input data. They also allow us to anticipate the worst-case scenarios that our algorithm should be able to handle without leading to inefficiencies or failures, such as exceeding the time limit or the memory limit.

In the context of the current problem:

  • The constraint on x (i.e., \(1 \leq x \leq 9\)) specifies the minimum and maximum value that can be pushed into the queue. Knowing this, we can evaluate whether our solution would handle all possible values of x. This constraint is important to consider when dealing with edge cases.

  • The constraint on the number of function calls (i.e., at most 100 calls will be made to push, pop, peek, and empty) informs us about the maximum operations our solution should handle efficiently. A solution with a time complexity of \(\mathcal{O}(n)\), where \(n\) is the number of operations, would likely be acceptable.

  • The stipulation that all calls to pop and peek functions will be valid simplifies the problem by indicating that we do not need to consider scenarios where these functions are called on an empty queue. This eliminates the need for additional error checking in our implementation.

Test Cases#

  • Test Case 1:

    • Operations: push(5), push(6), push(7), pop(), push(8), peek(), pop(), pop(), push(9), empty()

    • Queue states: [], [5], [5,6], [5,6,7], [6,7], [6,7,8], [6,7,8], [7,8], [8], [8,9], [8,9]

    • Expected Output: None, None, None, 5, None, 6, 6, 7, None, False

    • Explanation: After each push and pop operation, the queue state is updated. The peek operation does not change the queue state. The empty operation returns False since the queue is not empty.

  • Test Case 2:

    • Operations: push(2), push(4), pop(), push(6), pop(), pop(), empty()

    • Queue states: [], [2], [2,4], [4], [4,6], [6], [], []

    • Expected Output: None, None, 2, None, 4, 6, True

    • Explanation: After each push and pop operation, the queue state is updated. The empty operation returns True as the queue is empty.

Edge Cases#

  • Edge Case 1:

    • Operations: push(1), pop(), pop()

    • Queue states: [], [1], [], []

    • Expected Output: None, 1, Error message

    • Explanation: After pushing 1 and popping it, the queue is empty. Then the pop() operation tries to remove an element from the empty queue. This should ideally throw an error or return a specific value indicating that the operation is not valid.

  • Edge Case 2:

    • Operations: push(1), push(2), push(3), push(4), push(5), pop(), pop(), pop(), pop(), pop(), empty()

    • Queue states: [], [1], [1,2], [1,2,3], [1,2,3,4], [1,2,3,4,5], [2,3,4,5], [3,4,5], [4,5], [5], [], []

    • Expected Output: None, None, None, None, None, 1, 2, 3, 4, 5, True

    • Explanation: This case tests the FIFO behavior of the queue after a sequence

Solution (Using Two Stacks)#

A queue operates on the principle of First In First Out (FIFO), meaning that the elements that are inserted first are the ones that get removed first. Commonly, queues are implemented using linked lists, with new elements being added to the rear and removed from the front. However, in this instance, we are implementing a queue using two stacks, which inherently operate on a Last In First Out (LIFO) basis. Here, elements are added and removed from the same end, known as the top.

To emulate the FIFO behavior of a queue using stacks, we need two of them. These two stacks collaboratively work to reverse the order of element arrival, effectively transforming the LIFO behavior of a stack into the FIFO behavior of a queue. Consequently, one of the stacks ends up holding the queue elements in the order they should logically be in if we were using a traditional queue structure. This innovative use of two stacks provides an alternative approach to implementing a queue data structure.

Implementation using List#

Hide code cell source

 
 1from typing import List
 2
 3
 4class MyQueue:
 5    """
 6    Class that implements queue using two stacks (enqueue and dequeue).
 7
 8    Attributes
 9    ----------
10    enqueue : List[int]
11        Stack for enqueue operation (push to back of queue).
12    dequeue : List[int]
13        Stack for dequeue operation (remove from front of queue).
14    """
15
16    def __init__(self) -> None:
17        """Initializes an empty queue."""
18        self.enqueue: List[int] = []
19        self.dequeue: List[int] = []
20
21    def push(self, x: int) -> None:
22        """
23        Pushes an integer x to the back of the queue.
24
25        Parameters
26        ----------
27        x : int
28            The integer to be added to the back of the queue.
29        """
30        self.enqueue.append(x)
31
32    def move(self) -> None:
33        """
34        Transfers elements from the enqueue stack to the dequeue stack.
35        """
36        while not self.is_stack_empty(self.enqueue):
37            self.dequeue.append(self.enqueue.pop())
38
39    def pop(self) -> int:
40        """
41        Removes an integer from the front of the queue and returns it.
42
43        Returns
44        -------
45        int
46            The integer at the front of the queue.
47
48        Raises
49        ------
50        IndexError
51            If both stacks are empty, indicating the queue is empty.
52        """
53        if self.is_stack_empty(self.dequeue):
54            self.move()
55        return self.dequeue.pop()
56
57    def peek(self) -> int:
58        """
59        Returns the integer at the front of the queue without removing it.
60
61        Returns
62        -------
63        int
64            The integer at the front of the queue.
65        """
66        if self.is_stack_empty(self.dequeue):
67            self.move()
68        return self.dequeue[-1]
69
70    def is_stack_empty(self, stack: List[int]) -> bool:
71        """
72        Checks if the provided stack is empty.
73
74        Parameters
75        ----------
76        stack : List[int]
77            The stack to be checked.
78
79        Returns
80        -------
81        bool
82            True if the stack is empty, False otherwise.
83        """
84        return not stack
85
86    def empty(self) -> bool:
87        """
88        Checks if the queue is empty.
89
90        Returns
91        -------
92        bool
93            True if the queue is empty, False otherwise.
94        """
95        return self.is_stack_empty(self.enqueue) and self.is_stack_empty(self.dequeue)

A small test suite is provided below to check the correctness of the algorithm.

Consider the case where we push 1,2,3,4 and then pop the first in queue and then push 5, 6 to queue again and then pop the next in queue.

Our implementation still work in that case. Here’s the step-by-step breakdown:

  1. You push 1, 2, 3, 4 to the queue. Now, self.enqueue = [1, 2, 3, 4] and self.dequeue = [].

  2. You execute pop(). Because self.dequeue is empty, you pop each element from self.enqueue to self.dequeue, resulting in self.enqueue = [] and self.dequeue = [4, 3, 2, 1]. Then you pop from self.dequeue, so you get 1, and self.dequeue = [4, 3, 2].

  3. Now, you push 5 and 6 to the queue. So, self.enqueue = [5, 6] and self.dequeue = [4, 3, 2].

  4. If you execute pop() again, it will pop from self.dequeue since it’s not empty, and you get 2. After the operation, self.enqueue = [5, 6] and self.dequeue = [4, 3].

  5. If you keep popping until self.dequeue is empty, and then execute pop() again, it will transfer elements from self.enqueue to self.dequeue just like before.

Hide code cell source

 
 1from rich import print
 2
 3queue = MyQueue()
 4queue.push(1)
 5queue.push(2)
 6queue.push(3)
 7queue.push(4)
 8print(queue.pop())
 9queue.push(5)
10queue.push(6)
11print(queue.pop())

1

2

Implementation using Stack Class#

Hide code cell source

 
  1from __future__ import annotations
  2
  3import math
  4from IPython.display import display
  5from typing import Generator, List, Union, Any
  6from rich.pretty import pprint
  7
  8import sys
  9from pathlib import Path
 10
 11def find_root_dir(current_path: Path | None = None, marker: str = '.git') -> Path | None:
 12    """
 13    Find the root directory by searching for a directory or file that serves as a
 14    marker.
 15
 16    Parameters
 17    ----------
 18    current_path : Path | None
 19        The starting path to search from. If None, the current working directory
 20        `Path.cwd()` is used.
 21    marker : str
 22        The name of the file or directory that signifies the root.
 23
 24    Returns
 25    -------
 26    Path | None
 27        The path to the root directory. Returns None if the marker is not found.
 28    """
 29    if not current_path:
 30        current_path = Path.cwd()
 31    current_path = current_path.resolve()
 32    for parent in [current_path, *current_path.parents]:
 33        if (parent / marker).exists():
 34            return parent
 35    return None
 36
 37root_dir = find_root_dir(marker='omnivault')
 38
 39if root_dir is not None:
 40    sys.path.append(str(root_dir))
 41    from omnivault.dsa.stack.concrete import StackList
 42    from omnivault._types._generic import T
 43else:
 44    raise ImportError("Root directory not found.")
 45
 46
 47class MyQueue:
 48    """
 49    Class that implements queue using two stacks (enqueue and dequeue).
 50
 51    Attributes
 52    ----------
 53    enqueue : StackList[int]
 54        Stack for enqueue operation (push to back of queue).
 55    dequeue : StackList[int]
 56        Stack for dequeue operation (remove from front of queue).
 57    """
 58
 59    def __init__(self) -> None:
 60        """Initializes an empty queue."""
 61        self.enqueue: StackList[int] = StackList()
 62        self.dequeue: StackList[int] = StackList()
 63
 64    def push(self, x: int) -> None:
 65        """
 66        Pushes an integer x to the back of the queue.
 67
 68        Parameters
 69        ----------
 70        x : int
 71            The integer to be added to the back of the queue.
 72        """
 73        self.enqueue.push(x)
 74
 75    def move(self) -> None:
 76        """
 77        Transfers elements from the enqueue stack to the dequeue stack.
 78        """
 79        while not self.enqueue.is_empty():
 80            self.dequeue.push(self.enqueue.pop())
 81
 82    def pop(self) -> int:
 83        """
 84        Removes an integer from the front of the queue and returns it.
 85
 86        Returns
 87        -------
 88        int
 89            The integer at the front of the queue.
 90        """
 91        if self.dequeue.is_empty():
 92            self.move()
 93        return self.dequeue.pop()
 94
 95    def peek(self) -> int:
 96        """
 97        Returns the integer at the front of the queue without removing it.
 98
 99        Returns
100        -------
101        int
102            The integer at the front of the queue.
103        """
104        if self.dequeue.is_empty():
105            self.move()
106        return self.dequeue.peek()
107
108    def empty(self) -> bool:
109        """
110        Checks if the queue is empty.
111
112        Returns
113        -------
114        bool
115            True if the queue is empty, False otherwise.
116        """
117        return self.enqueue.is_empty() and self.dequeue.is_empty()

Hide code cell source

 
1queue = MyQueue()
2queue.push(1)
3queue.push(2)
4queue.push(3)
5queue.push(4)
6print(queue.pop())
7queue.push(5)
8queue.push(6)
9print(queue.pop())

1

2

Push#

The newly arrived element is always added on top of stack enqueue, see Fig. 59.

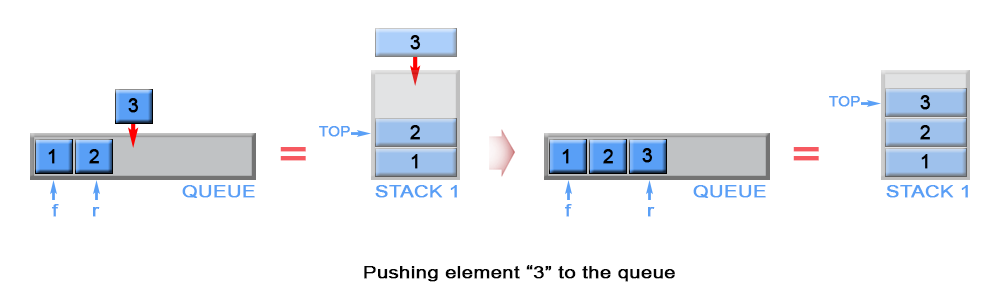
../../../_images/232_queue_using_stacksAPush.png

Fig. 59 Pushing an element onto the queue enqueue stack.#

Code Breakdown#

This push method is a part of the MyQueue class, which implements a queue using two stacks: enqueue and dequeue.

Let’s break down what this push function is doing:

def push(self, x: int) -> None:
    """
    Pushes an integer x to the back of the queue.

    Parameters
    ----------
    x : int
        The integer to be added to the back of the queue.
    """
    self.enqueue.append(x)

The push method appends an integer x to the enqueue stack, which is used as the main storage for incoming elements.

This mimics the behavior of a queue’s enqueue operation, adding an element to the back of the queue. In a typical queue implementation, new elements are always added to the end (or back) of the queue. Here, we simulate this by pushing new elements onto the enqueue stack.

Time Complexity#

The time complexity of the push operation in this queue implementation is \(\mathcal{O}(1)\). This is because the push operation essentially involves an append operation to the end of the enqueue list, which is a constant time operation in Python.

To understand this in a more practical sense, consider the following line from the push method:

self.enqueue.append(x)

This line performs an append operation on the enqueue list. In Python, appending to the end of a list is a constant time operation, meaning it takes a constant amount of time to execute, regardless of the size of the list. Therefore, the time complexity of the push operation is \(\mathcal{O}(1)\).

Table 58 Time Complexity of Push Operation#

Case

Complexity

Worst Case

\(\mathcal{O}(1)\)

Average Case

\(\mathcal{O}(1)\)

Best Case

\(\mathcal{O}(1)\)

Space Complexity#

Table 59 Space Complexity of Push Operation#

Type

Complexity

Description

Auxiliary Space

\(\mathcal{O}(n)\)

The enqueue and dequeue stacks which help in the operations of the queue can grow with the number of elements, which is \(n\).

Total Space

\(\mathcal{O}(n)\)

The total space is the sum of the input and auxiliary space. Since the input space is \(\mathcal{O}(1)\) (no data given at the start), the total space complexity remains \(\mathcal{O}(n)\).

Note carefully we treated both the enqueue and dequeue stacks as auxiliary space. This is because they are not part of the input, but rather are used to help in the operations of the queue.

Pop#

When the queue needs to be popped, we flip the enqueue stack and pour it into the dequeue stack, see {numref}232_queue_using_stacksAPop for a visual representation.

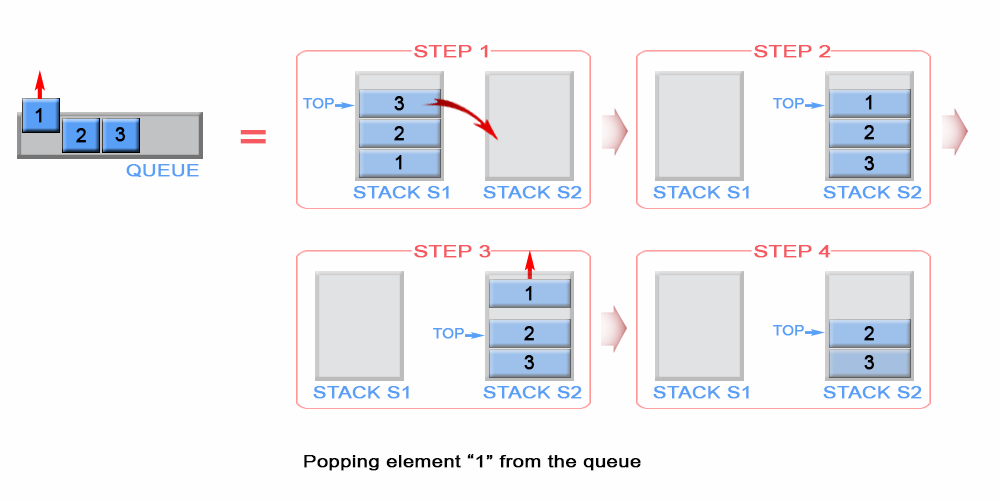
../../../_images/232_queue_using_stacksAPop.png

Fig. 60 Popping an element from the queue dequeue stack.#

Code Breakdown#

This pop method is a part of the MyQueue class, which implements a queue using two stacks: enqueue and dequeue.

Let’s break down what this pop function is doing:

def pop(self) -> int:
    """
    Removes an integer from the front of the queue and returns it.

    Returns
    -------
    int
        The integer at the front of the queue.

    Raises
    ------
    IndexError
        If both stacks are empty, indicating the queue is empty.
    """
    if self.is_stack_empty(self.dequeue):
        self.move()
    return self.dequeue.pop()

The pop method simulates the behavior of a queue’s dequeue operation, removing an element from the front of the queue. If the dequeue stack is empty, it calls the move method to transfer all elements from the enqueue stack to the dequeue stack, reversing their order to maintain the correct queue order. It then pops and returns the top element from the dequeue stack, which corresponds to the front of the queue.

Time Complexity#

The time complexity of the pop operation is not always constant because it depends on whether the dequeue stack is empty. If the dequeue stack is not empty, then popping an element off the dequeue stack is a constant time operation, \(\mathcal{O}(1)\).

However, if the dequeue stack is empty, we need to transfer all elements from the enqueue stack to the dequeue stack using move method, which takes \(\mathcal{O}(n)\) time, where \(n\) is the number of elements in the enqueue stack.

However, if we use amortized analysis, we see that for \(n\) push operations, there could be at most \(n\) pop operations that transfer elements from enqueue to dequeue. Thus, in an amortized sense, each pop operation takes constant time, giving us an amortized time complexity of \(\mathcal{O}(1)\) for the pop operation.

Table 60 Time Complexity of Pop Operation#

Case

Complexity

Worst Case

\(\mathcal{O}(n)\)

Amortized Case

\(\mathcal{O}(1)\)

Best Case

\(\mathcal{O}(1)\)

Space Complexity#

The reason that the space complexity of the pop operation is considered \(\mathcal{O}(1)\) is because the pop operation itself does not require any additional space that scales with the size of the input.

When you call the pop method, it does not create any new data structures or variables that depend on the size of the input (the number of elements in the queue). Even when the pop operation triggers the move operation, no new space is allocated; instead, the existing space in the enqueue and dequeue stacks is reorganized.

The enqueue and dequeue stacks already exist as part of the queue’s storage, so their space usage is considered part of the total space complexity of the queue, not the auxiliary space complexity of the pop operation. The auxiliary space complexity considers only the additional space required to perform the operation, beyond the space already used to store the input.

So, while the total space complexity of the MyQueue class is \(\mathcal{O}(n)\), where n is the number of elements in the queue, the space complexity of the pop operation is \(\mathcal{O}(1)\) because it doesn’t require any additional space beyond what’s already used to store the elements in the queue.

Table 61 Space Complexity of Pop Operation#

Type

Complexity

Description

Auxiliary Space

\(\mathcal{O}(1)\)

See explanation above.

Total Space

\(\mathcal{O}(1)\)

The total space is the sum of the input and auxiliary space. Since the input space is \(\mathcal{O}(1)\) (no data given at the start), the total space complexity remains \(\mathcal{O}(1)\).

Armortized Analysis#

We will use s1 to represent the enqueue stack and s2 to represent the dequeue stack for the following analysis.

I was genuinely confused by the amortized analysis of the pop operation when I first encountered it. I didn’t understand how we could say that the amortized time complexity of the pop operation was \(\mathcal{O}(1)\) when the worst-case time complexity was \(\mathcal{O}(n)\) (seemingly).

Firstly, amortized time complexity is different from the worst-case time complexity. For the worst-case time complexity, we look at the scenario where the most unlucky thing can happen (i.e. finding the desired number only at the last element of a list). However, for the amortized time complexity, we average the time taken by all operations in a sequence, this sequence can be defined as the worst-case sequence of operations[1].

The basic idea is that a worst case operation can alter the state in such a way that the worst case cannot occur again for a long time, thus amortizing its cost.

The key to understanding why these queue operations have O(1) amortized time complexity is understanding that each individual element is only moved once from the enqueue stack to the dequeue stack.

Let’s consider a sequence of \(n\) push operations followed by \(n\) pop/peek operations:

\[ \underbrace{\text{enqueue(1), enqueue(2), ..., enqueue(n)}}_{\text{enqueue operations}}, \overbrace{\text{dequeue(1), dequeue(2), ..., dequeue(n)}}^{\text{dequeue operations}} \]

  1. Each push operation is clearly O(1). And so \(n\) push operations are \(\mathcal{O}(n)\).

  2. The worst case time complexity of a single pop operation is \(\mathcal{O}(n)\), since we have \(n\) pop operations, the total time complexity is \(\mathcal{O}(n^2)\).

Remark 73 (Analyzing Time Complexity with Worst Case Only)

If we only consider the worst-case time complexity for the pop operation, it could lead us to an overly pessimistic time complexity estimate.

Here’s a breakdown of the scenario:

  • We begin with an empty queue.

  • We push \(n\) elements into the queue. Each push operation has a time complexity of \(\mathcal{O}(1)\), so \(n\) push operations have a time complexity of \(\mathcal{O}(n)\).

  • We then pop all \(n\) elements from the queue. Each pop operation could potentially have a worst-case time complexity of \(\mathcal{O}(n)\) when the s2 stack is empty.

Now, if we were to look only at the worst-case time complexity of the pop operation, we might think that popping \(n\) elements from the queue would have a time complexity of \(\mathcal{O}(n^2)\), because for each pop operation we’re considering its worst-case scenario, which is \(\mathcal{O}(n)\), and we’re doing this \(n\) times.

However, this would be overly pessimistic as the bound given by the worst case analysis is very “loose”. In reality, the worst-case scenario for a pop operation (i.e., the s2 stack being empty and needing to move all elements from s1 to s2) only happens once for every \(n\) push operations. After the elements have been moved to s2, all the remaining pop operations have a time complexity of \(\mathcal{O}(1)\) until s2 becomes empty again. In other words, the number of times pop operation can be called is limited by the number of push operations before it.

Therefore, the overall time complexity for \(n\) pop operations is not \(\mathcal{O}(n^2)\), but closer to \(\mathcal{O}(n)\), leading to an amortized time complexity of \(\mathcal{O}(1)\) per operation. Let’s proceed to prove it.

Example 51 (Amortized Time Complexity of Queue Operations)

Let’s break down the operations and their costs:

  • Each push operation costs \(1\) unit of time, as it involves a single append operation to the end of stack s1. Therefore, \(n\) push operations cost \(n\) units of time.

  • The first pop operation after a sequence of push operations is more expensive, as it involves popping all elements from stack s1 and pushing them to stack s2. This costs \(2n\) units of time (one for each pop from s1, and one for each push to s2).

  • However, once the elements are in stack s2, each subsequent pop operation only costs \(1\) unit of time, as it simply involves popping an element off the top of s2. Therefore, \(n - 1\) such pop operations cost \(n - 1\) units of time.

So, the total cost of performing \(n\) push operations and \(n\) pop operations is

\[ \underbrace{n}_{\text{push to s1}} + \underbrace{2n}_{\text{pop from s1 and push to s2}} + \underbrace{n - 1}_{\text{pop from s2}} = \underbrace{4n - 1}_{\text{total time units}} \]

However, we performed \(2n\) operations in total (each push and each pop is considered an operation), so the average cost per operation is

\[ \frac{\overbrace{4n - 1}^{\text{time units}}}{\underbrace{2n}_{\text{operations}}} = 2 - \frac{1}{2n} \]

Note carefully the difference in units, the numerator is in time units, while the denominator is in number of operations. So the end result is in time units per operation, which coincides with the definition that on average, each operation takes \(2 - \frac{1}{2n}\) time units.

So when you compute \(\frac{(4n - 1)}{2n}\), you’re effectively asking: “On average, how many computational steps (time units) does each operation take?” This is the definition of amortized time complexity.

As \(n\) approaches infinity (which is usually the case when we talk about time complexity), the \(\frac{1}{2n}\) term becomes negligible, and so the amortized time complexity is approximately \(2\), which is a constant. Therefore, we say that the amortized time complexity is \(\mathcal{O}(1)\).

\[ \lim_{{n \to \infty}} \left(2 - \frac{1}{2n}\right) = 2 \]

or more concisely,

\[ \lim_{{n \to \infty}} \mathcal{O}\left(2 - \frac{1}{2n}\right) = \mathcal{O}(1) \]

The concept of amortized analysis is used in algorithms to show that while an operation might be expensive in the worst case, over time, the average cost per operation is much lower.

In this scenario, the expensive operation (pop operation when s2 is empty) does not happen very often - it only happens when all elements need to be transferred from s1 to s2, which happens once for every \(n\) operations. Thus, the cost of this expensive operation is “amortized” over the \(n\) operations, resulting in an average cost of \(\mathcal{O}(1)\) per operation.

Peek#

Same as pop, except we don’t remove the element from s2.

Empty#

Both s1 and s2 must be empty for the queue to be empty. The time and space complexity of the empty operation are both trivial, \(\mathcal{O}(1)\).

References and Further Readings#

Contents